Intrinsic equation 1: , b non zero. Intrinsic equation 2:  , . Cartesian parametrization: ,  () Transcendental curve.

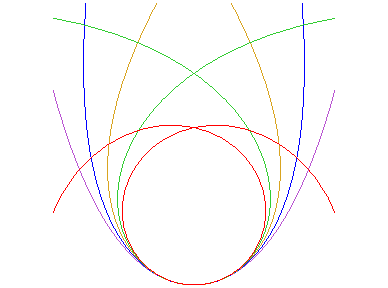
Alysoids are curves such that when we let them run on a straight line, the centre of curvature of the curve at the contact point describes a parabola of axis perpendicular to the line, not meeting this line (here, the parabola ); see at curve of Mannheim.
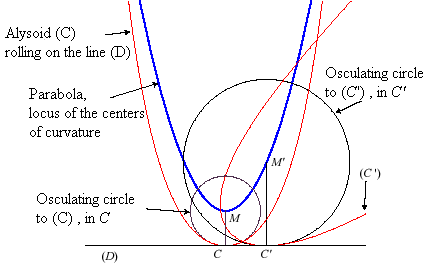When a = b (k = 1), we obtain the catenary:.
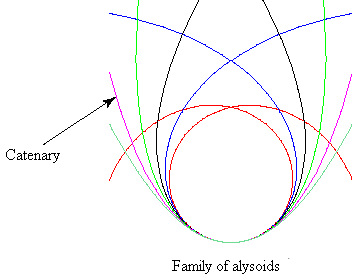When a = 2b (k = 1/2), we obtain the parametrization:

In the case where b would be zero, we would obtain a different curve, particular case of pseudo-spiral of Pirondini, named "antiloga", whose characteristics follow:

Cartesian parametrization: ().

 
 

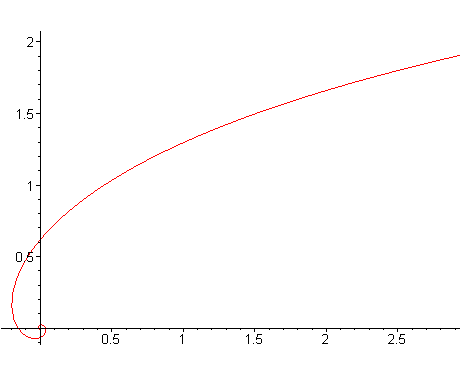next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2016