Negative podal

NEGATIVE PEDAL or ORTHOCAUSTIC
Pedal in blue, negative pedal in red

Let M₀ be the current point on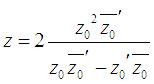

. The current point M on the negative pedal with fixed point O is defined by

which results in :

in Cartesian coordinates,

in complex parametrization, and

in polar coordinates, with

; here

(see notations).

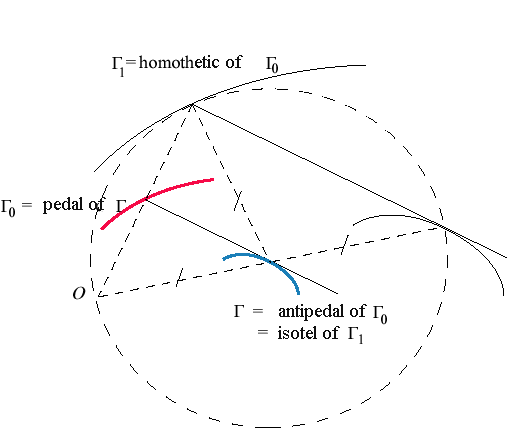
The negative pedal of a curve with fixed point O is the curve whose pedal is the initial curve. See the bottom of this page for a kinematic interpretation of this definition.

The negative pedal of a curve with fixed point O is therefore the envelope of the lines perpendicular at the point M to the lines (OM), as M describes , hence the equivalent name of orthocaustic.
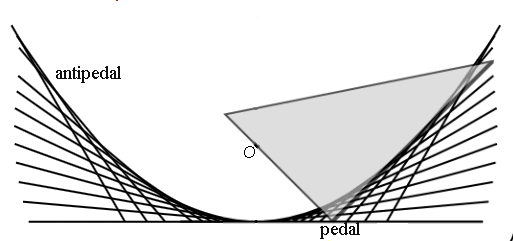
The negative pedal is also the equidistant curve of O and the homothetic transformation of with ratio 2 and center O. From this point of view, the negative pedal is called the isotel curve of .

If the vertex of a try square describes the initial curve with one of the sides bound to pass through O, then the other side envelopes the negative pedal.
Remark : the points on the side of the try square that passes through O describe conchoids of the initial curve, and the points on the other side describe isoconchoids. See glissette.

The negative pedal with fixed point O is also the reciprocal polar of the inverse, for any circle with center O.

Examples :
    - the orthocaustics of straight lines are parabolae (focus at O, the initial line being the tangent at the vertex)
    - the orthocaustics of circles are ellipses or hyperbolae depending on whether O is inside or outside the circle (focus at O, the initial circle being the principal circle of the conic)
    - the negative pedal of a parabola with its focus as fixed point is Tschirnhausen's cubic
    - the negative pedal of an ellipse with its center as fixed point is Talbot's curve
    - the negative pedal of the involute of a circle with its center as fixed point is the inverse caustic of the circle

See more examples at pedal !

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

The negative pedal of a curve with fixed point O is therefore the envelope of the lines perpendicular at the point M to the lines (OM), as M describes , hence the equivalent name of orthocaustic. The negative pedal is also the equidistant curve of O and the homothetic transformation of with ratio 2 and center O. From this point of view, the negative pedal is called the isotel curve of .
If the vertex of a try square describes the initial curve with one of the sides bound to pass through O, then the other side envelopes the negative pedal. Remark : the points on the side of the try square that passes through O describe conchoids of the initial curve, and the points on the other side describe isoconchoids. See glissette.