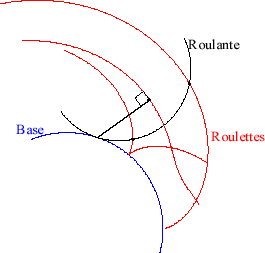
The base curve of the movement of a plane over a fixed plane is the curve generated on the fixed plane by the instant centre of rotation of the moving plane. The rolling curve is the curve generated by this point on the moving plane. During the movement, the rolling curve rolls without slipping on the base, which is its envelope. The roulettes (or trajectories) are the curves traced on the fixed plane by the points of the moving plane. The straight line joining the contact point between the base and the rolling curve and the tracing point is orthogonal to the roulette (Descartes' theorem). See some examples of the study of the movement of a plane over a fixed plane on this page, as well as the notion of glissette, that is useful for defining different movements of a plane over a fixed plane. When the movement of the plane is a translation, the base and the rolling curve are located at infinity (see crawl curve).

Let  be the reference frame of the plane and  be its moving frame at time t; the affix of the point  is  and the affix of the vector  is  in the reference frame. The affix of a point M = M(t) is m=m(t) in the reference frame and  in the moving frame, with the relation: , which leads, by derivating with respect to time, to  (1) . Let N(t, u), of affix n(t, u), be the point whose position in the moving frame at time t is the position of the point M at time u. We have: .

At time t, the instant centre of rotation  of the moving frame with respect to the reference frame, which also is the current point on the base, is the fixed point, in the moving frame, at zero speed with respect to the reference frame. It is thus defined by , which yields, thanks to (1), , that is to say . The affix  of B in the moving frame is defined by , hence . We can then prove that , which shows that the rolling curve rolls without slipping on the base. The rolling curve is, at any time t, the curve described by the points of affix  in the moving frame, as u describes . The affix of the current point  (R is to B what N is to M above) in the reference frame is: . A roulette is the trajectory of a point M fixed in the moving frame. It is defined by  ( being constant here). Example of calculation of a roulette, knowing the base and the rolling curve, for the cycloid: parameters  ;  can be written , hence , and , so that: .

Here is, in the case where the vectors  and  are collinear, the calculation of the base, the rolling curve and the roulettes, when the movement of the plane is defined by the trajectory of the point W (polar equation). Therefore, the base's polar equation is  and the rolling curve's Cartesian parametrization is .

Examples:

    - When the moving plane is the plane tied to the tangent of a curve, the base is the evolute of this curve, and the rolling curve is the normal. The curve is one of the roulettes.
    - When the rolling curve is the reflection of the base with respect to a tangent, the roulette is the orthotomic curve of the base with respect to the reflection of the tracing point across the tangent (this point is fixed); for example:
        - the roulettes of the centre of an ellipse rolling on the reflection of an ellipse are Booth's ovals
        - the roulettes of the centre of a hyperbola rolling on the reflection of a hyperbola are Booth's lemniscates
        - the roulette of the vertex of a parabola rolling on the reflection of a parabola is Diokles' cissoid
An exhaustive list of examples is located at pedal.

    - The examples where the base is a line can be found on this specific page.
    - When the rolling curve is a line and the tracing point is on the line, the roulette is an involute of the base.
    - When a roulette is a line, the base and the rolling curve form a wheel-road couple, whereas when a roulette is circular, the base and the rolling curve have mating gear profiles.

Other examples:
 

base	rolling curve	tracing point	roulette
circle	circle	on the rolling circle	centred cycloid
circle	circle	any	centred trochoid
circle	line	located on the half plane containing the circle, at a distance from the line equal to the radius of the circle	Archimedean spiral
circle	equiangular spiral	pole of the spiral	circle concentric to the base
catenary	line	see figure on the right	line (base of the catenary)
parabola	Kampyle	on the transversal axis of the Kampyle	conchoid of Nicomedes
Kampyle	parabola		kappa
quadrifolium	ellipse		double egg
cycloid	cardioid	pole of the cardioid	involute of cycloid

Remark: even when the base and the rolling curve are algebraic, the roulette can be transcendental (cf. cycloid).

More generally, the notion of roulette of a fixed curve on the moving plane refers to the envelope of this curve in the fixed plane. The curvature centres of theses two curves are related through the Euler-Savary theorem.
Examples:
    - the base is the envelope of the rolling curve (which is the only curve that does not slip on the roulette).
    - the directrix of a parabola rolling on a line envelopes the catenary traced by its focus.
    - a diameter of a circle rolling without slipping on a line envelopes a cycloid, and any line of the moving plane envelopes an involute of cycloid.
    - a diameter of a circle rolling without slipping on the interior of a circle of double radius envelopes an astroid, and the line perpendicular to this diameter at one of its extremities envelopes a Maltese cross; more generally, with circles of any radius, the envelopes of the diameter of the rolling circle are the centred cycloids and the envelopes of any straight line are involutes of centred cycloids.
    - the negative pedal of a curve is the roulette of the perpendicular at the point M to the line (OM), when M describes the curve, the moving plane being the plane in which M and (OM) are fixed.

The movement of a sphere over an isometric sphere gives rise to notions of base, rolling curve and roulettes absolutely similar to the case of the movement of a plane over a fixed plane. See for example the spherical trochoids of second type.
 
 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL 2017