Bifolium

BIFOLIUM

Curve studied by de Longchamps in 1886 and Brocard in 1887.
Other names: double folium, bifoliate curve.

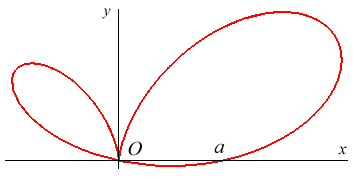Polar equation:

.
Cartesian equation:

.
Rational Cartesian parametrization:

.
Rational circular quartic.

Let (C) be the circle passing through O, A(a,0) and B(0, b), and a variable line passing through O and intersecting (C) in P, whose projection on Ox is H. The associated bifolium is the locus of the projection M of H on the line (OP).

Bifoliums are the pedal curves of deltoids with respect to one of their points (here O); see the links between the bifolium and the deltoid at folium.

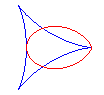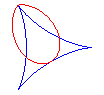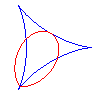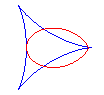
When a = 0, i.e. when the pedal is taken with respect to a cusp of the deltoid, we get the regular bifolium.
When b = 0, i.e. when the pedal is taken with respect to a vertex of the deltoid, we get the simple folium.

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra