| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
BRACHISTOCHRONE OF GIVEN LENGTH
| Problem posed and solved by Jean
Bernoulli in 1718, and studied by Nathan
Moscovitch in 1934.
Other name: isoperimetric brachistochrone. |
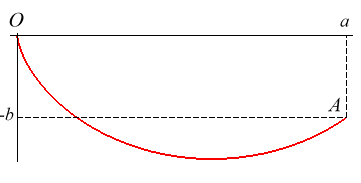
| The brachistochrone of given length is the curve of length l on which a massive point without initial speed must slide without friction in a uniform gravitational field in such manner that the travel time is minimal among all the curves of length l joining two fixed points O and A (here A(a, -b)). | |
Initial problem: 
minimal, for given  .
Differential equation (obtained by applying the Euler-Lagrange equation):  .
(see here for a little more detail) Parametrization: 
where 
and  (for
k = 0, we find the usual brachistochrone,
in other words the cycloid).
Curvilinear abscissa given by:  .
Travel time 
given by:  .
Other parametrization: |
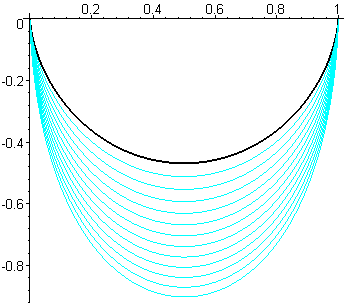
| View of various brachistochrones joining O = (0,
0) and A = (a, 0) for k between –1 and 1, and
a
= 1.
When k approaches –1, the limit curve is the segment line [OA], of length a and infinite travel time. For k = 0, (limit between red and green), we get the cycloid of length 
and minimal travel time  .
For k = 1 (bottommost curve), we get a curve of length 5a/2 and travel time  (rational
curve, as noted by Bernoulli).
Relation between c and a:  .
Length of a complete arch: |
 |
| View of various brachistochrones joining O = (0,
0) and A = (a, 0) for k > 1 and a = 1.
Relation between c and a: Length of a complete arch: |
 |
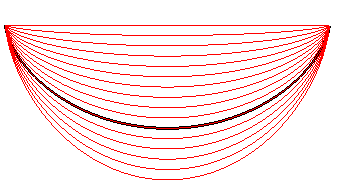
Remark: these curves also solve the dual problem of determining
the curve of given travel time with minimal length.
| Comparison between the curves obtained by solving the differential equation (on the left) and mere scalings of the cycloid (on the right).... |  |
 |
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017
.
.
.
.
.
.
.