CAYLEY OVAL
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
CAYLEY OVAL

| Curve studied by Cayley in 1857.
Arthur Cayley (1821-1895): British mathematician. |
| Bifocal equation: Cartesian equation : Cartesian parametrization : |
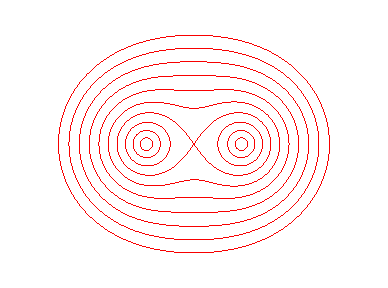
Cayley ovals are the loci of the points on the plane for which the harmonic mean of the distances to two points, the foci, is constant (= b).
Therefore, they are the equipotential lines of the electrostatic potential created by two equal charges placed at the foci (or of the gravitational potential created by two identical masses).
 view of the equipotential lines, in red, with the field lines.
view of the equipotential lines, in red, with the field lines.
Case b < a: the "oval" is composed of
two egg-like shaped curves symmetrical about O.
Case e = 1 (b = a): the curve is
shaped like an 8.
Case :
the oval has the shape of an "ellipse" that is worn out at the summits
of the minor axis.
Case :
the oval finally has the shape of an oval, leaning towards a circular shape
as e increases.
All this reminds strongly of the Cassinian
ovals (who, themselves, are quartics); these two families can indeed
be placed into the more general framework of loci of points on a plane
for which the order p mean of the distances to 2 points is constant,
with bifocal equation
; we can see above that Cassini and Cayley ovals are quite close; they
can be distinguished by their tangents at O.
|
|
|
|
|
|
|
|
|
|
b = 0: foci, b = a: two tangent circles |

b = 0: 2 points, b = a: eight |
b = 0: 2 points, b = a: eight |
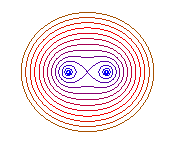
b = 0: 2 points, b = a: eight |
|
|
|
|
|
|
|
|
|
|
|

b = 0: 2 points, b = a: eight |
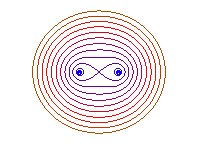
b = 0: 2 points, b = a: eight |
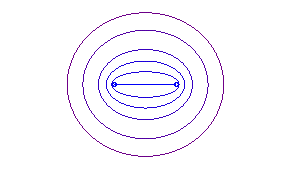
b = a: segment line |
|
|
|
|
|
|
|
|
|
|
|
|
|

b = a: point O |
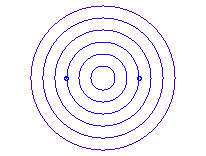
b = a: point O |
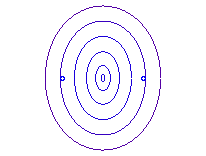
b = a: point O |

b = a: point O |
|
|
|
Another generalisation consists in placing any charge
at any point; the equipotential lines, with multifocal equation
are called Cayley equipotential lines: they are, to Cayley ovals,
what Cassinian curves are
to Cassinian ovals.
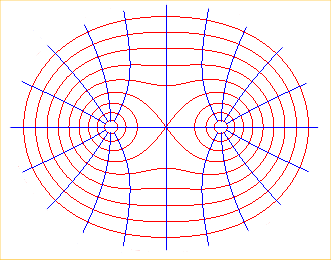
Here are, for example, the equipotential lines (in red)
with equation
and the corresponding field lines (in blue) in the case of two particules
of opposite charges.
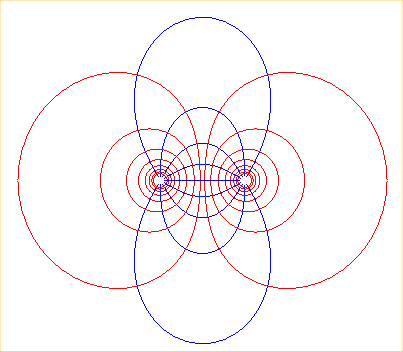
For the limit case of these latter curves, when the poles come closer and closer to each other, see the curve of the dipole.
Of course, this can be generalised to curves with multifocal
equation
that result in Cayley equipotential lines when p = – 1. When p
= – 2, we get the "equal-loudness" curves. They are the curves joining
the points where the acoustic intensities, due to sound sources placed
at the poles, are equal. See for example the isophonic curves for sources
placed at the vertices of a triangle:

For other equipotential and field lines, see this page.

The Cayley owl....
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2023