Cayley's sextic

CAYLEY'S SECTIC

Curve studied by Maclaurin in 1718 and Cayley in 1867.
Arthur Cayley (1821-1895): British mathematician.

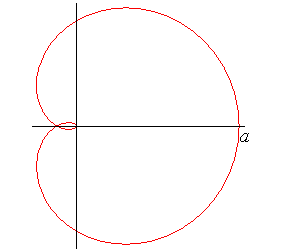Polar equation: .
Rational Cartesian parametrization: (t = tan q ).
Cartesian equation: .
Tricircular. rational. sextic.
Curvilinear abscissa: .
Radius of curvature: .
Pedal equation: .
Length: .

Cayley's sextic is the pedal of the cardioid with respect to its cuspidal point (here, the cardioid is ).

It also is the inverse of the Tschirnhausen cubic with respect to its focus.

It is an example of sinusoidal spiral and it can also be seen as the locus of the vertex of a parabola tangent to a fixed circle with its focus on this circle (here, the circle with centre O and radius 2a).

Its evolute is the nephroid centred on (a/2, 0) and passing through O.

Since the evolute of a nephroid still is a nephroid, Cayley's sextic is one of the nephroid's parallel curves.