COCHLEOID
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
COCHLEOID

| Curve studied by Wallis in 1685, Peck in 1700, Bernoulli
in 1726, Cesaro in 1878 and Falkenburg in 1884.
In its Latin form cochlea, the name is due to Wallis, and in its current form, to Falkenburg. The Latin term cochlea comes from the Greek kokhlias: shell, snail (cf. the cochlea in the internal ear, and the cuiller, instrument used to eat snails). |
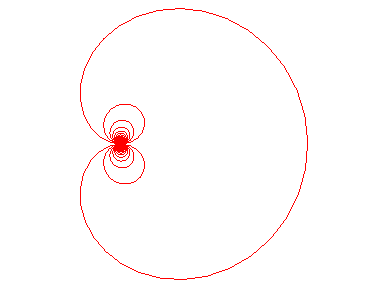
| Polar equation: Cartesian parametrization: Cartesian equation: Polar tangential angle: Transcendental curve. |
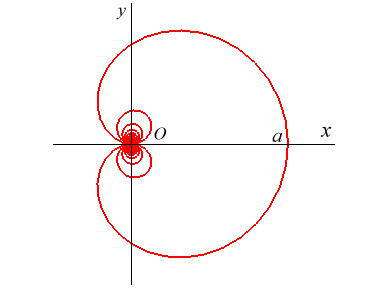 |
| The cochleoid is the locus of the extremity of an arc of a circle of fixed length a while the other end is fixed and tangent to a fixed straight line. In concrete terms, one can imagine the curve described by the extremity of a plastic pipe with a circular shape when the other end is fixed. |
 |
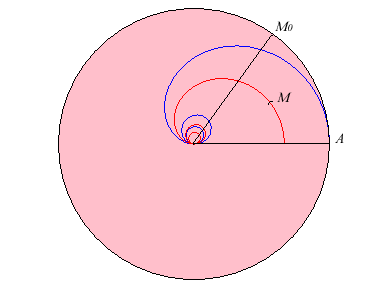
| The cochleoid is also the barycentric
curve of the circle. More precisely, it is the locus of the gravity
centre M of a homogeneous massive wire wrapped around the circle
with centre O and radius a (one of its extremities being
at A with polar coordinates (a, 0) and the other at |

The point M is the gravity centre of the arc AM0 |
| The gravity centre of the circular sector delimited by
[OA] and [OM0] also is a
homothetic cochleoid with ratio 2/3: |
 |
| The cochleoid is also the inverse with respect to O
and with power of inversion a2 of
the quadratrix of Dinostrate: |
 |
| When a point N describes the hyperbolic
spiral In other words, the cochleoid is a part of the strophoidal curve of the hyperbolic spiral; the other part, described by |
 |
| The cochleoid is the limit curve of the curves of complex
parametrization : |
 |
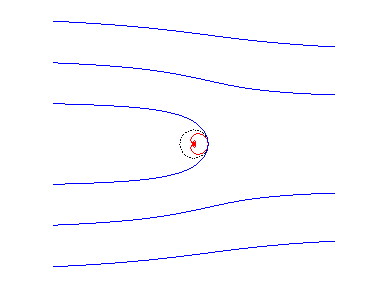
The cochleoid is one of the conical perspectives of a
circular
helix, the centre of perspective being a point on the helix and the
projection plane being perpendicular to its axis. As a result, the inferior
part of the cochleoid represents the view, in perspective, of a helix traced
on a cylindrical tube, when looking from the ceiling.
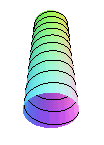 |
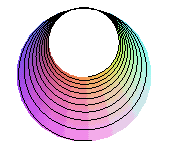
the tube when looking from the ceiling: we get the cochleoid |

looking from the centre: we get the hyperbolic spiral |
The contact points of the tangents to the cochleoid inclined
by an angle
with respect to (Ox) are located on the strophoid
,
which is a right strophoid when
and is reduced to a circle for
.
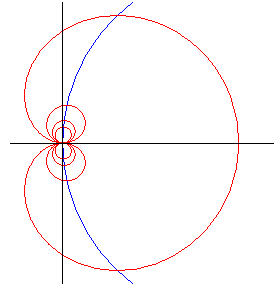
the points with horizontal tangent are located on a circle |
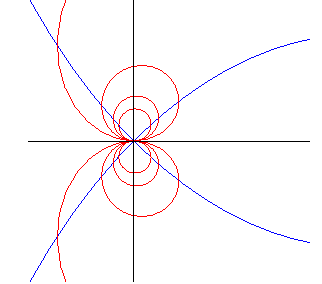
the points with vertical tangent are located on a right strophoid |

the points with given oblique tangent are located on an oblique strophoid. |
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017