Conchoid of a conic

FOCAL CONCHOID OF A CONIC

For a conic with eccentricity e and parameter a, and a conchoid with modulus ka:
Polar equation: (general form: ).
Cartesian equation: .
Rational quartic.

The focal conchoids of conics are the conchoids of conics with respect to one of their foci.

Case of an ellipse

Case of a parabola

Case of a hyperbola

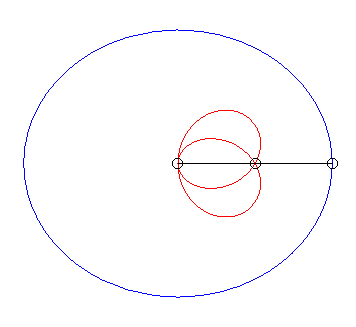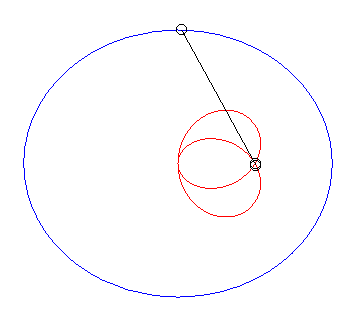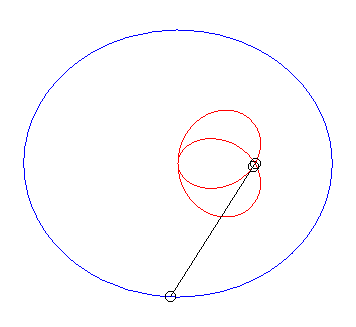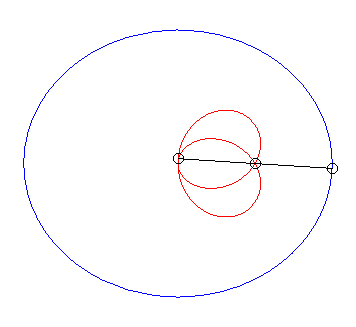When (i.e. when the modulus ka of the conchoid is the opposite of the semi-major axis), we get Jerabek's curves.

When k = –1 (i.e. when the modulus of the conchoid is the opposite of the parameter of the conic), we get the curves with a double point where the tangents coincide.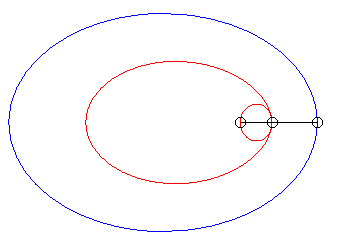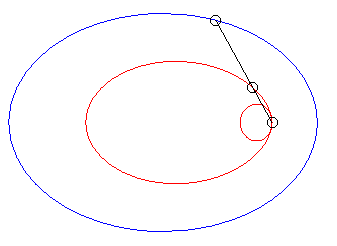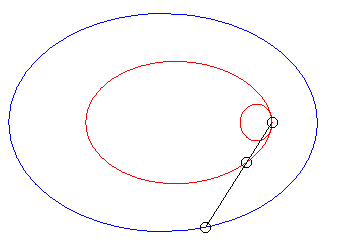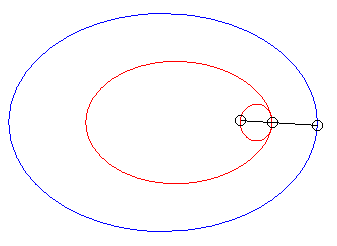

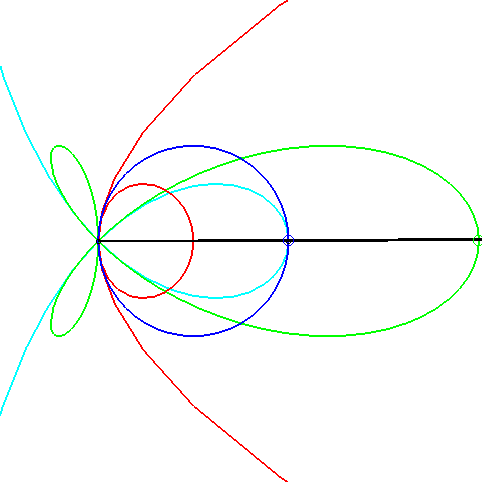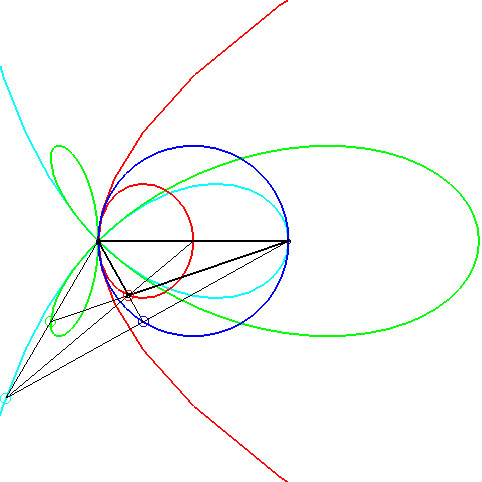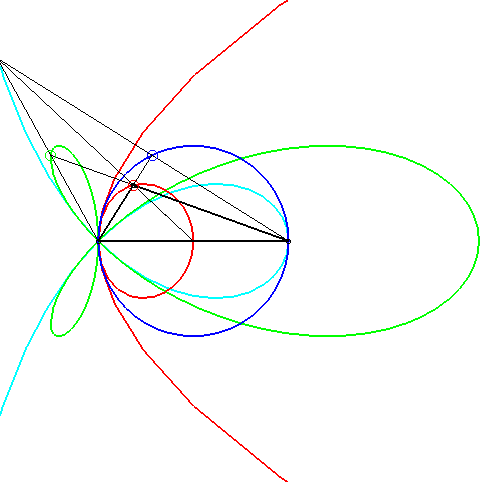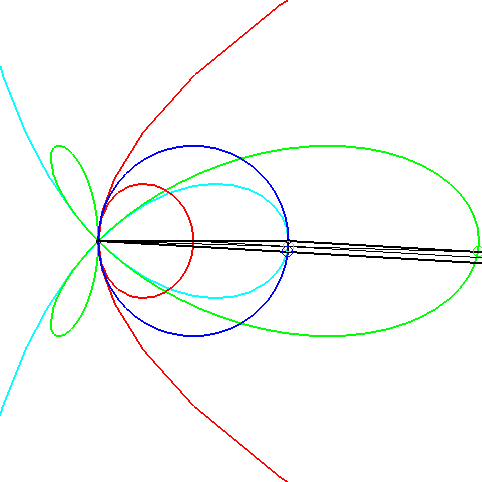
When (i.e. when the modulus of the conchoid is the opposite of the distance of the focus to the summit), we get the curves with a cuspidal point.

A conchoid of a parabola with k = –1 arises in the problem of determining the triangles such that the intersection of the median passing by a vertex, the altitude passing by another, and one of the bisectors passing by the last is not empty.
When the side cutting the median line is fixed, the opposite vertex describes a conchoid of a parabola (in red, opposite); the extremity of the bisector describes a torpedo, the intersection point, a strophoid (in light blue, opposite), and the extremity of the altitude, of course, a circle.

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

When (i.e. when the modulus ka of the conchoid is the opposite of the semi-major axis), we get Jerabek's curves.
When k = –1 (i.e. when the modulus of the conchoid is the opposite of the parameter of the conic), we get the curves with a double point where the tangents coincide.
When (i.e. when the modulus of the conchoid is the opposite of the distance of the focus to the summit), we get the curves with a cuspidal point.