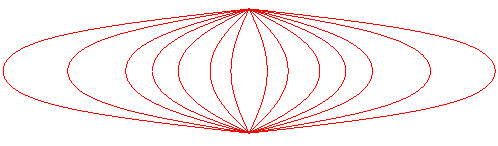
SKIPPING ROPE CURVE
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
SKIPPING ROPE CURVE

| Curve studied by Clebsch in 1860.
Other name: troposkein. Ref: [greenhill] p. 97. |
The skipping rope curve is the shape taken by an inextensible homogeneous flexible massive wire in rotation around an axis attached to two points on this axis (gravity is ignored). It is impossible for the naked eye to tell it and an arch of a sinusoid apart, and yet it is the plot of the Jacobi elliptic function noted sn, and not that of the sine function.
It can be proved that the skipping rope curve with extremities
A
and B and length L is also the curve of length L joining
A to B such that the moment of inertia with respect to the
axis (AB) is maximal.
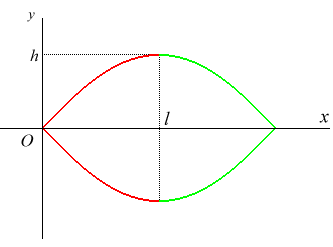 |
Differential equation: Cartesian equation: Cartesian parametrization written with the elliptic function of the first kind F (EllipticF in Maple) : Cartesian equation written with the Jacobi elliptic function sn (JacobiSN in Maple) : Slope at O: Abscissas of the summits: Length of an arch: |
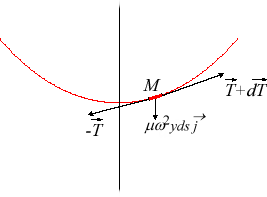 |
With the notation of the opposite figure ( This simplifies to |
In the equation,
if the exponent 1/2 is replaced by 3/2, we get the lintearia.
For another curve plotting an elliptic function of Jacobi,
see wheel-road couple.

 |
 |
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017