Involute of a circle

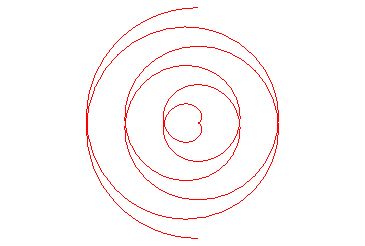
INVOLUTE OF A CIRCLE

Other name: anti-clothoid.

Cartesian parametrization:

(involute of the circle with centre O and radius a, with a contact at (a, 0)).
Complex parametrization:

.
Polar parametrization:

(with

).
Polar equation:

.
Cartesian tangential angle:

.
Curvilinear abscissa:

.
Radius of curvature:

.
Intrinsic equation 1:

.
Intrinsic equation 2:

.
Pedal equation:

.
Cartesian differential equation:

The definition of this curve is given by its name (see involute)!

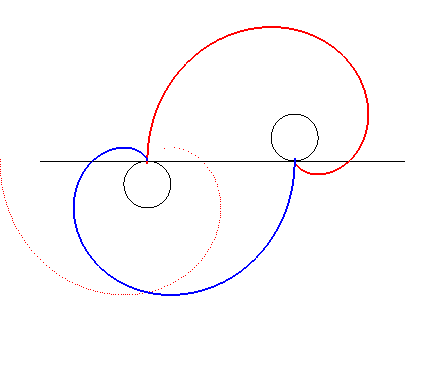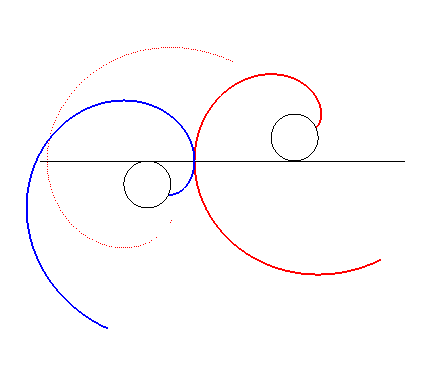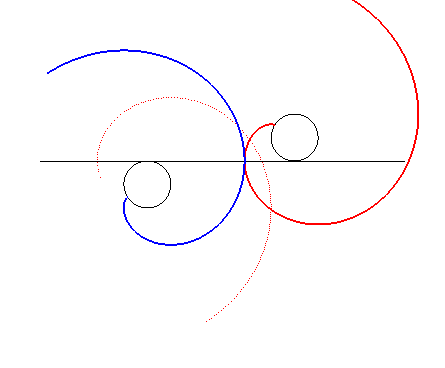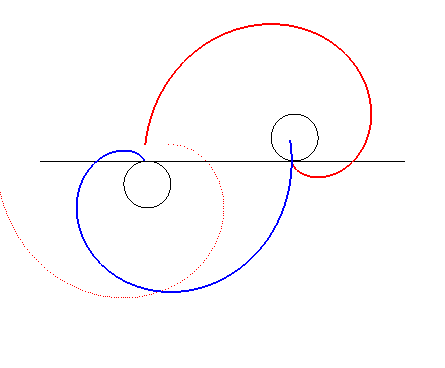
The involute of a circle is the curve for which all the normals are tangent to a fixed circle.
More practically, it is the curve traced by a hand unwinding a wire reel held in the other hand.

Conversely, if an involute of a circle turns around the centre of the generating circle, every tangent to the circle remains always normal to the involute.

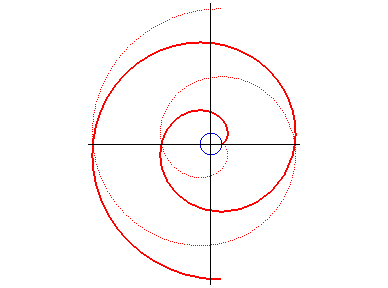
For large values of t, the Archimedean spiral with equation is the asymptotic curve to the involute of a circle. It also is its pedal with respect to O.

This last property has the following consequence: if an involute of a circle is turned uniformly around its centre, then the tangents to the involute having a given direction move in a uniform translation motion: it is the reason why the profile of cams is an involute of a circle.

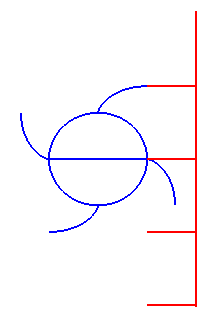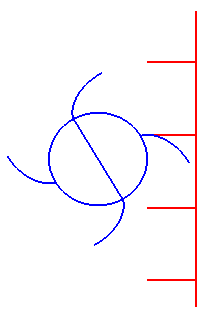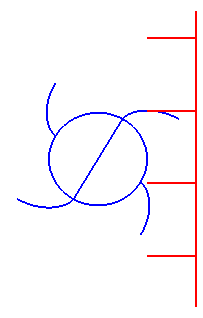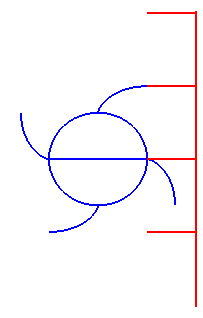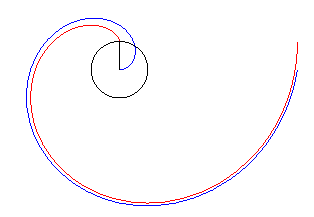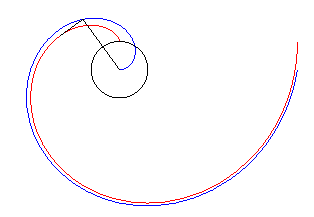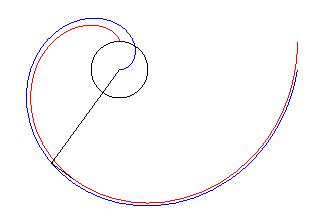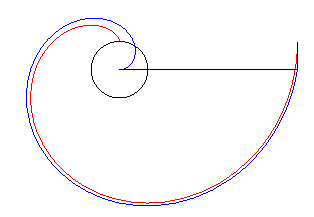
The involute of a circle also has a kinematic definition, due to the formulae : it is the curve for which, when it is travelled along in a uniformly varying movement, the rotation speed of the tangent is constant (hence its name anti-clothoid, because the clothoid, is the curve for which, when it is travelled along in a uniform movement, the rotation speed of the tangent is linear).

Another kinematic definition:
A person P is walking on a stage turning at constant speed around a point O; the movement of P on the stage is linear and uniform with speed v and does not pass by O. If v = k w /a where a is the distance between the line along which P travels and O, the trajectory of P is given by . Therefore, it is an involute of a circle when k = 1.
Conversely, the trace of a marble rolling freely on the stage (thus with a linear uniform motion in the fixed frame) is such a curve.

Case k = 1: involute of a circle. Case k = -1.

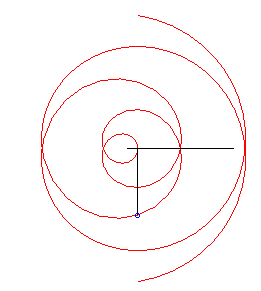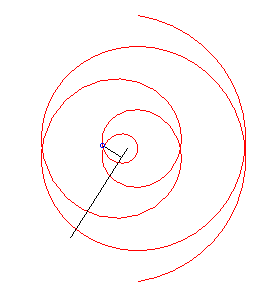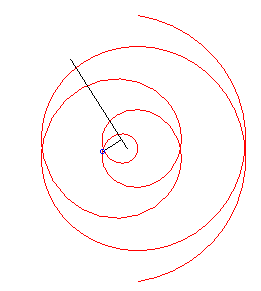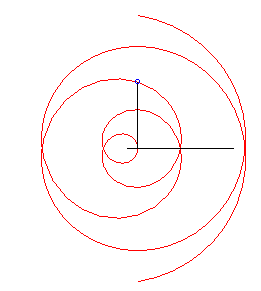
Like any family of involutes of the same curve, the involutes of a circle are parallel to one another (by the way, the involute of a circle is the only curve isometric to its parallel curves).
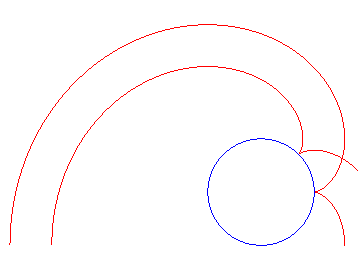More precisely, the image by a rotation by an angle of the involute gives a parallel curve at distance .

In the special case , we get the same curve; the involute of a circle is therefore an auto-parallel curve; its coils are at distance from one another.
This implies that if we translate an involute of a circle by perpendicularly to its symmetry axis, we draw the line joining the two cusps, and we spin both the involutes at the same speed around their centres, they will remain in contact, perpendicularly to that line.

This was applied to design gears (composed here of three portions of involutes of circles each) called paradoxical gears, because they turn in the same way.
Make sure to follow the contact points on the black lines.

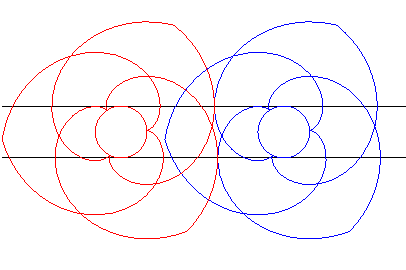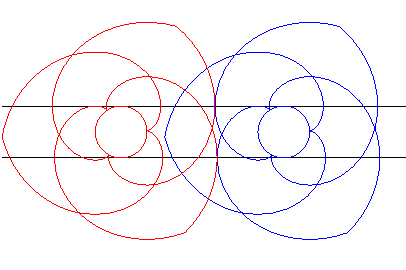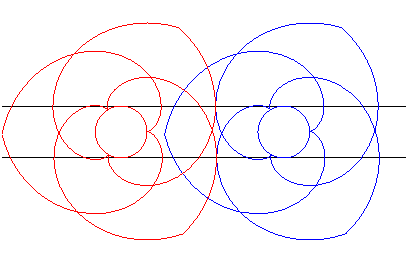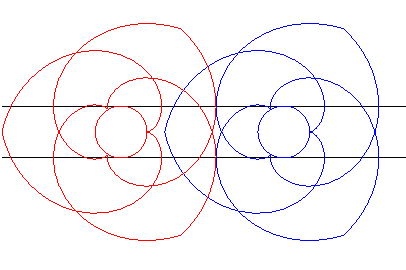
Animation made by J. Lefort

Let us now apply to the translated involute a symmetry about the common normal; both the involutes remain in contact, but turn in opposite ways.
Remark: the curves slip on one another at the contact point (it is not on the line joining the two centres of rotation) but this is negligible enough so that it does not cause overheating problems in practice. Therefore, these are not mating profiles.

The same gears as above are placed this time on both sides of the line and thus turn in the opposite way.
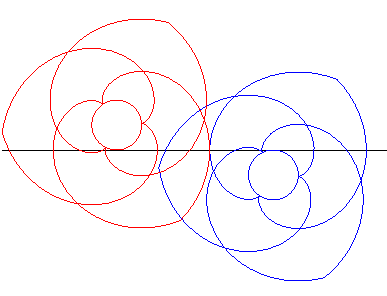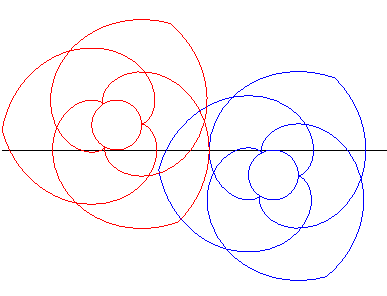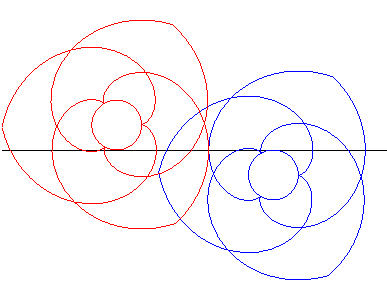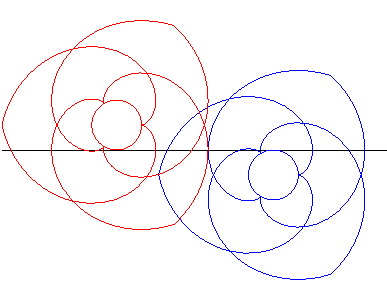
Animation made by J. Lefort

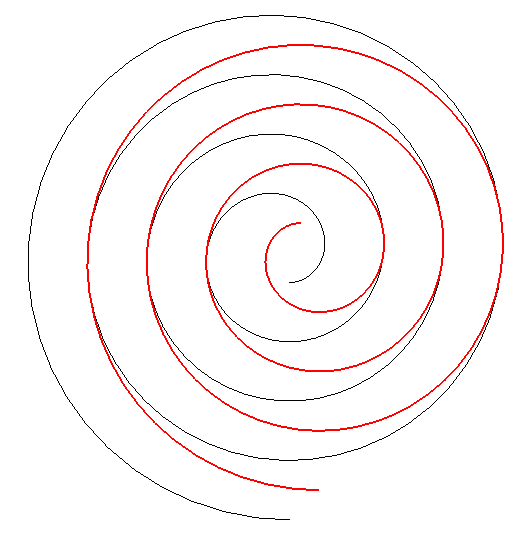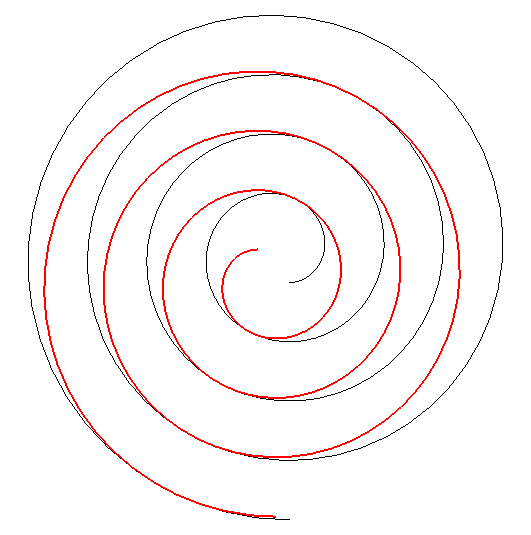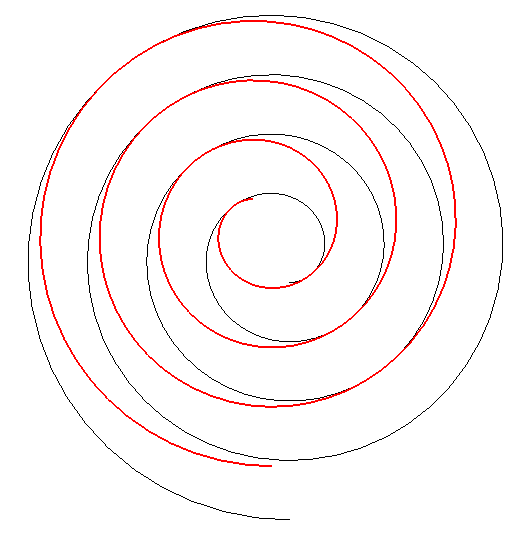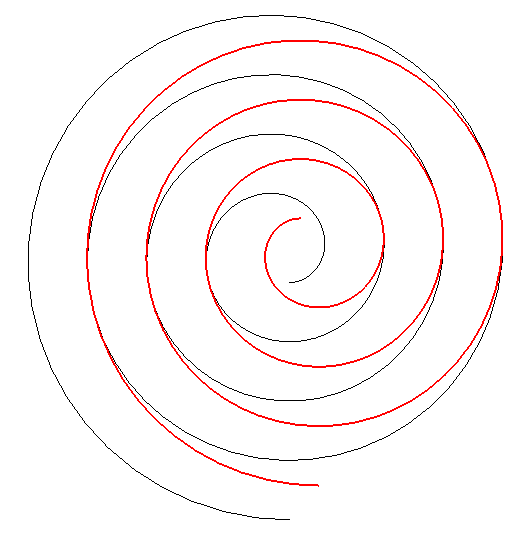
Another special case of parallel curve: the symmetrical involute about the centre of the circle is parallel to the initial curve, at distance (it is, in a way, the central curve of the initial involute). Therefore, a circle with radius centred on an involute of a circle envelopes the symmetrical involute.

By duality from the previous property, we get the following one: consider an involute of a circle with radius a and centre O; if this involute is translated (in red below) in such a way that its centre describes a circle with centre O and radius , then the envelope of the family of curves obtained is the symmetrical involute of a circle with respect to O and the initial involute. And there are an infinite number of tangency points (2 by coil).
Advice: follow with your eyes a tangency point. This property, discovered by Léon Creux (cf. patent in 1905 and article in 1911) is used in the fabrication of gas compressors called spiral compressors, or scroll compressors.
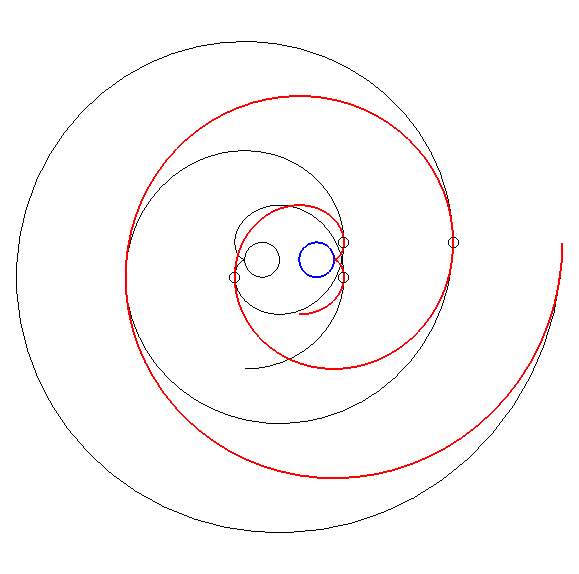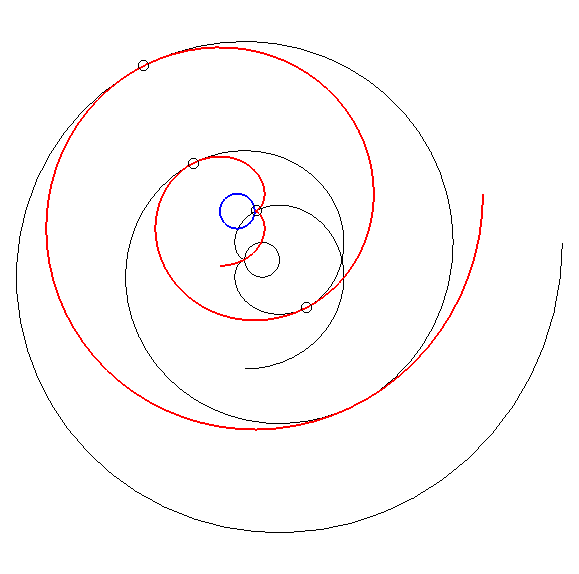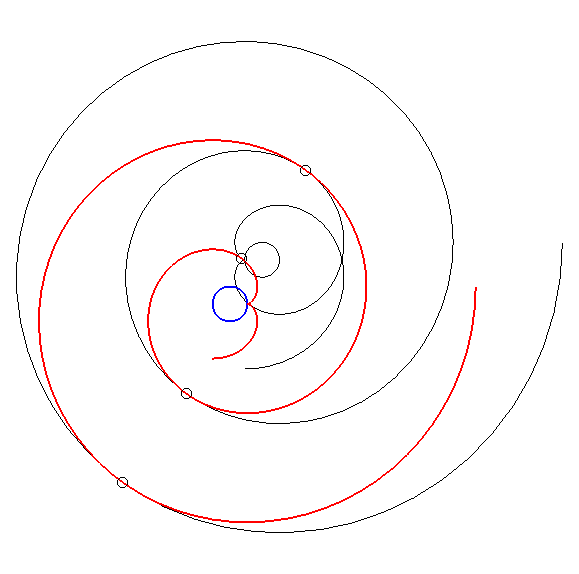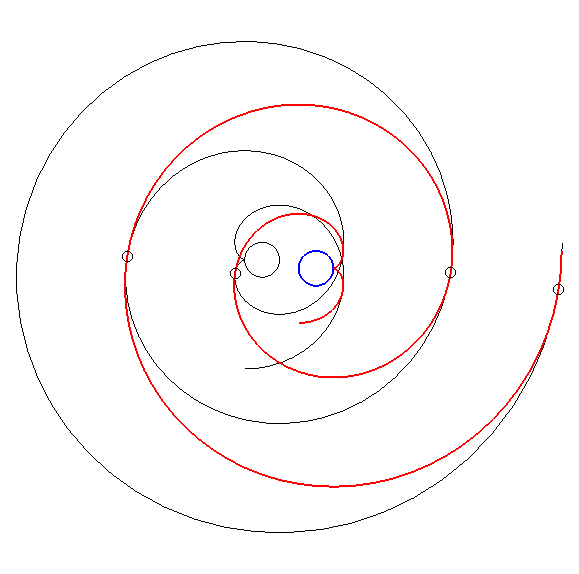The family of moving spirals is defined by and the characteristic points are given by .

Animation showing the use of involutes of circles for classic gears. The involutes stay in contact on a tangent common to both the circles.

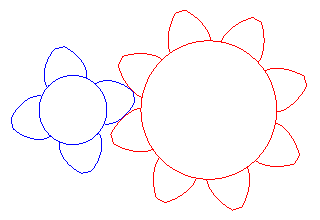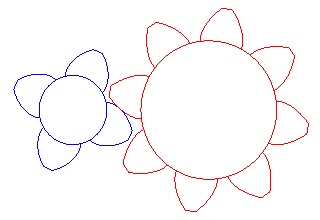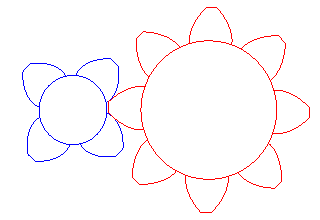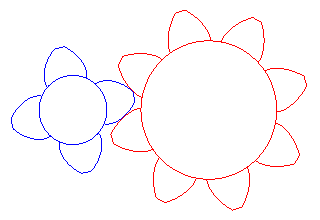The section of the developable helicoid by a plane perpendicular to the axis is an involute of a circle.

The projection of an helix of the paraboloid of revolution is an involute of a circle.

The involute of a circle is a sectrix and a quadratrix.

Its inverse with respect to its centre is the tractrix spiral, and its negative pedal is the inverse caustic of a circle.

Its involutes are the curves for which the radius of curvature is equal to the distance to O, plus a constant, one of them being the Norwich spiral.

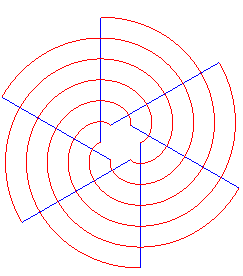
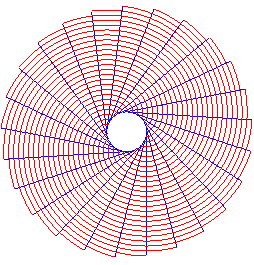
The half-involutes of a given circle form a double orthogonal system together with the half-tangents to the circle

Gears in involutes of circles made by Vincent Viton.

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

The involute of a circle is the curve for which all the normals are tangent to a fixed circle. More practically, it is the curve traced by a hand unwinding a wire reel held in the other hand.
Conversely, if an involute of a circle turns around the centre of the generating circle, every tangent to the circle remains always normal to the involute.

For large values of t, the Archimedean spiral with equation is the asymptotic curve to the involute of a circle. It also is its pedal with respect to O.
This last property has the following consequence: if an involute of a circle is turned uniformly around its centre, then the tangents to the involute having a given direction move in a uniform translation motion: it is the reason why the profile of cams is an involute of a circle.

Like any family of involutes of the same curve, the involutes of a circle are parallel to one another (by the way, the involute of a circle is the only curve isometric to its parallel curves). More precisely, the image by a rotation by an angle of the involute gives a parallel curve at distance .
In the special case , we get the same curve; the involute of a circle is therefore an auto-parallel curve; its coils are at distance from one another. This implies that if we translate an involute of a circle by perpendicularly to its symmetry axis, we draw the line joining the two cusps, and we spin both the involutes at the same speed around their centres, they will remain in contact, perpendicularly to that line.
This was applied to design gears (composed here of three portions of involutes of circles each) called paradoxical gears, because they turn in the same way. Make sure to follow the contact points on the black lines.	Animation made by J. Lefort
Let us now apply to the translated involute a symmetry about the common normal; both the involutes remain in contact, but turn in opposite ways. Remark: the curves slip on one another at the contact point (it is not on the line joining the two centres of rotation) but this is negligible enough so that it does not cause overheating problems in practice. Therefore, these are not mating profiles.
The same gears as above are placed this time on both sides of the line and thus turn in the opposite way.	Animation made by J. Lefort
Another special case of parallel curve: the symmetrical involute about the centre of the circle is parallel to the initial curve, at distance (it is, in a way, the central curve of the initial involute). Therefore, a circle with radius centred on an involute of a circle envelopes the symmetrical involute.