next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

EVOLUTE OF A PLANE CURVE


Notion studied by Apollonius, around 200 BC then by Huygens in 1673.
Other names: focal curve, or caustic.

The evolute of a curve is the locus of its centres of curvature, or also the envelope of its normals.
 
For an initial curve  with current point , the evolute is the set of points .
Cartesian parametrization: 
Complex parametrization: .
If the initial curve's intrinsic equation 2 is , we get:
Parametric intrinsic equation 1: .
Intrinsic equation 2: .

Kinematic interpretation: the evolute is the base of the movement of a plane over a fixed plane, when the moving plane is linked to the tangent to the curve. The rolling curve is its normal, and therefore rolls without slipping on the evolute.
 
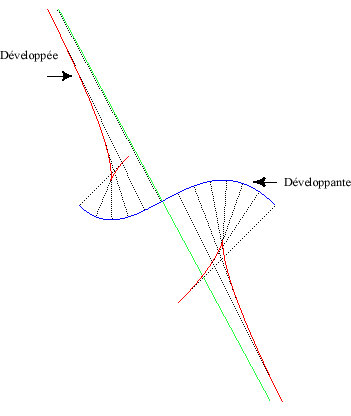The singularities of the evolute correspond to the vertices of the curve, i.e. to the extrema of the radius of curvature, notion that generalises that of a point located on a symmetry axis perpendicular to the tangent at this point.
Opposite, note that the radius of curvature has two nonzero minima and an infinite maximum. In the latter case, the singularity is at infinity, and the normal is the asymptote to the evolute.

The evolutes of two similar curves are similar (with the same similarity); the evolute of an algebraic curve is an algebraic curve.

Physical interpretation: considering the curve  as a light source, the evolute represents the locus where the rays emitted by this curve are concentrated. The evolute is therefore rather called caustic in optics (but see the similar definition of the caustic in math); it is also the locus of the singularities of wavefronts emitted by  (see at parallel curves).

The evolute of the orthotomic curve of  with respect to a point S (itself image of the pedal of  with respect to S by an homothety with centre S and ratio 2), is the caustic by reflection with centre S of , and to put it in a nutshell:

Evolute of pedal = caustic

Therefore, the evolutes of limaçons of Pascal and the caustics of circles are the same curves.
 

Examples:
 
initial curve evolute
ellipse  tetracuspid

with 
hyperbola  1/2 Lamé curve: with 
parabola  semicubical parabola
cycloid same cycloid, translated 
cardioid similar cardioid with ratio 1/3
nephroid similar nephroid with ratio 1/2
epicycloid with parameter q similar epicycloid with ratio q/(q+2)
deltoid similar deltoid with ratio 3
astroid similar astroid with ratio 2
hypocycloid with parameter q similar hypocycloid with ratio q/(q-2)
paracycloid hypercycloid
hypercycloid paracycloid
logarithmic spiral  logarithmic spiral 
tractrix catenary
tractrix spiral Catalan curve
catenary curve 
Cayley sextic nephroid
Norwich spiral involute of a circle

See also at involute, see a planar generalisation at evolutoid, see the notion of evolute of a 3D curve,  the notion of pedal surface and the notion of focal, which is to surfaces what the evolute is to curves.
 
next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

© Robert FERRÉOL 2017