Polar equation:. Cartesian equation: . Tricircular sextic of genus 1. Area of a ball: .

The curve of the dipole is the curve with the above polar equation, a special case of Clairaut's curve.

Its name comes from the fact that it is the shape assumed by the equipotential lines of an electrostatic dipole, in other words two opposite charges at infinitely small distance.
Indeed, if the charges are placed at A and B on Ox, the equipotential lines are the curves with equation , and when A and B go to O, , hence the equation  of the approximate equipotential lines.

It so happens that these curves also are the orthogonal curves of the field lines of an electromagnetic dipole.
 

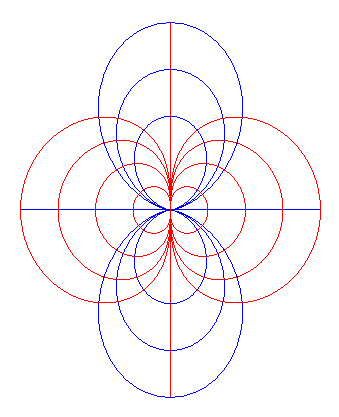First interpretation: the red curves of the dipole are the equipotential lines of an electrostatic dipole and the field lines are the blue double eggs. Second interpretation, the blue double eggs are the fielxd lines of a magnetic dipole (such as, for example, the Earth) and the orthogonal trajectories are the red curves of the dipole.

 
 

The curve of the dipole also is the locus of the centre of a lemniscate of Bernoulli constrained to remain tangent to a fixed line at a fixed point (see at glissette).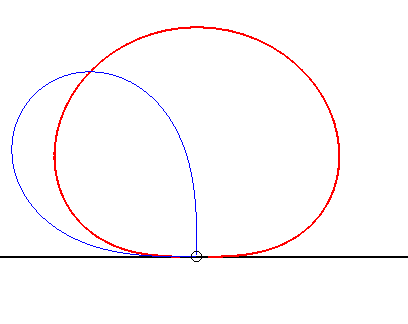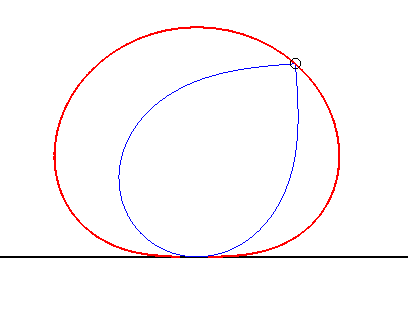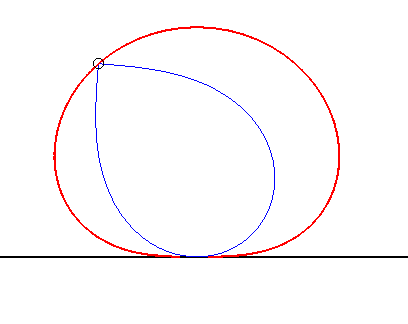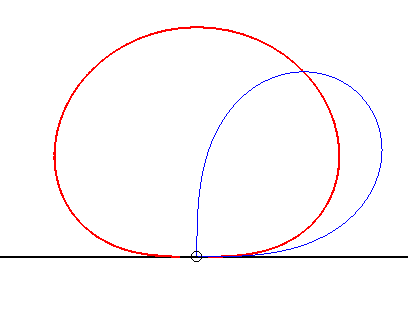

It is also the meridian of the surface of equal attraction, hence its name of curve of equal attraction.

Variation: the curve with equation (instead of ) was presented by Cundy and Rollett under the name "butterfly":

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2017