Cartesian equation:

The Doppler spiral is the trace on a fixed plane of a uniform spiral-like movement in a plane in uniform translation. The name "Doppler spiral" comes from the analogy with the Doppler effect concerning a wave whose emitter is moving.
If the moving plane is fixed (k = 0), the spiral is none other than an Archimedean spiral.
 
 

Case 0 < k < 1

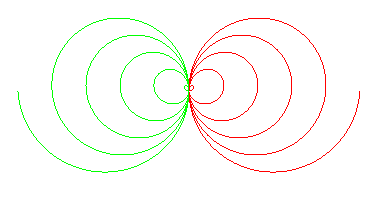
Case k = 1

Case k > 2

 
 

The Doppler spirals are the planar projections of the conical Pappus spirals.

 
 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL 2017