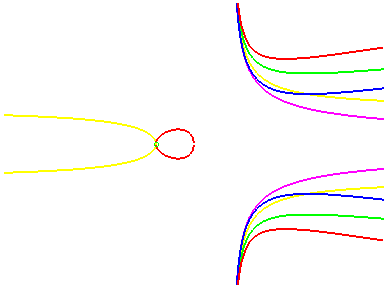
green: acnodal cubic
blue: elliptic cubic with a branch
yellow: crunodal cubic
magenta: cuspidal cubic
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
CUBICAL HYPERBOLA
 |
red: elliptic
cubic with an oval green: acnodal cubic blue: elliptic cubic with a branch yellow: crunodal cubic magenta: cuspidal cubic |
| Curve studied by Newton in 1701.
Other names: ambigene hyperbola (name given by Newton), half-trident. |
| Cartesian equation: Cubic. |
The homographic transformation:
reduces this cubic to the right
divergent parabola
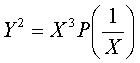
Like the divergent
parabolas (as well as the Chasles
cubics), the cubical hyperbolas represent the perspective views of
all cubics.
| When P is of degree 3, the cubical hyperbola is
rational iff P has a multiple root.
If, additionally, the leading coefficient is negative, then it can be constructed as a Rosillo curve. Remarkable cases: the cissoid of Diocles ( |
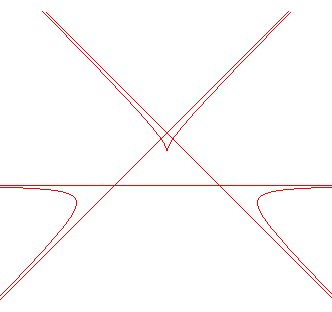
case where the leading curve is positive and a root has multiplicity 3: |
| Remarkable cubical hyperbolas in the case where P
is of degree 3 and has simple roots: the Lamé
cubic ( |

|
When P is of degree 2, we get the Hügelschäffer
eggs.
When P is of degree 1, we get the witch
of Agnesi ()
or the yellow curve above.
|
|
|
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017