| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
HYPERBOLISM AND ANTIHYPERBOLISM OF A CURVE
NEWTON TRANSFORMATION
| Notion studied by Newton. |
| Cartesian equation | Cartesian parametrization | |
| initial curve | |
|
| hyperbolism with respect to O and the line x = a | |
|
| antihyperbolism | |
|
 |
The hyperbolism of a curve 
with respect to a point O and a line (D) is the curve  ,
locus of the point M defined as follows: given a point (M0)
on , the
line (OM0)
cuts (D) at P; M is the projection of P on
the line parallel to (D) passing by M0.
Analytically, with the line (D) x = a, the
transformation of |
The inverse transformation 
,
is referred to as antihyperbolism.
Examples:
| antihyperbolism | O and (D) (for the initial curve) | O et (D) (for the final curve) | hyperbolism |
| circle | O on the circle, (D) tangent to the circle opposite to O | O on the "middle" of the asymptote and (D) tangent at the summit | witch of Agnesi |
| circle | O centre of the circle, (D) tangent to the circle | O at the centre and (D) tangent at the summit | Külp quartic |
| circle | (D) perpendicular to the line joining O
to the centre of the circle
(this case includes the previous ones) |
Granville egg | |
| circle | O on the circle, (D) parallel to the diameter passing by O | O at the centre and (D) passing by the intersection points with the circle | anguinea |
lemniscate of Gerono: 
(up to scaling in one direction) |
O at the centre, (D) tangent at a vertex | O at the centre, (D) tangent to the circle | circle |
| piriform quartic | O at the cusp, (D) perpendicular to the symmetry axis | O on the circle, (D) parallel to the tangent to the circle at this point | circle |
rational divergent
parabola:  |
O at the centre, (D): x = a | O at the centre and (D): x = a | parabola |
cubical
parabola:  |
O and line x = a | O and line x = a | trident: |
visiera: |
O and line x = a | O and line x = a | visiera: |
If the straight line (D) is replaced by any given
curve, we get the more general transformation of Newton:
 |
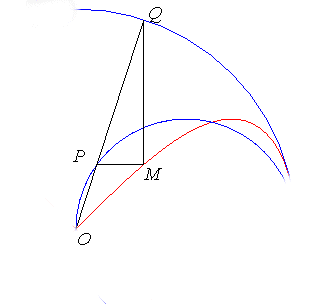The Newton transform of a couple of curves ( , )
with respect to a frame Oxy is the curve ,
locus of the point M defined as follows: a line (D) passing
by O cuts
at P and
at Q; M is the intersection point between the line parallel
to Ox passing by P and the line parallel to Oy passing
by Q.
We get the hyperbolism with
a line parallel to Oy. |
Cartesian parametrization of the Newton transform of
the curves 
and  with
respect to Oxy:  . |
Examples:
| first curve (G1) | second curve (G2) | transform |
| circle with centre O | circle with centre O | ellipse (obtained by "reduction of the ordinates") |
circle centred on Ox passing through O  |
circle with centre O |
eight-like curve  ,
dilatation of a lemniscate of Gerono
(not dilated when a = b, i.e. when the circles are tangent). |
| swap the previous circles | arc of a parabola | |
| circle centred on Ox | circle with centre O | Hügelschäffer egg |
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017
;
it is quadratic, so an algebraic curve of degree n is transformed
into an algebraic curve of degree £ 2n.