Polar equation: . For 0 < k = tha  <1: . For k = cotha  > 1: . Cartesian equation: . Polar equation in the frame centred on (a,0): Circular rational quartic.

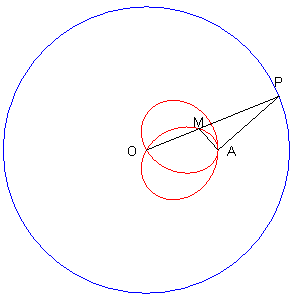
The Jerabek curve  is the locus of the end M of a right angle PAM, when the point P describes a circle (C) with centre O and radius a and the point M is on the line (OP) (here, A(a, 0) and OP = ka). Therefore, it is the base of the movement of a plane over a fixed plane a fixed point of which is P and a fixed line of which is (PA), this movement is called circular conchoidal movement.

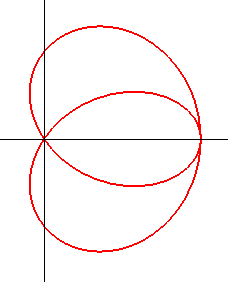
When A is inside the circle (k > 1), the curve is closed, included in the circle, and has a crunodal double point and a tacnodal double point.

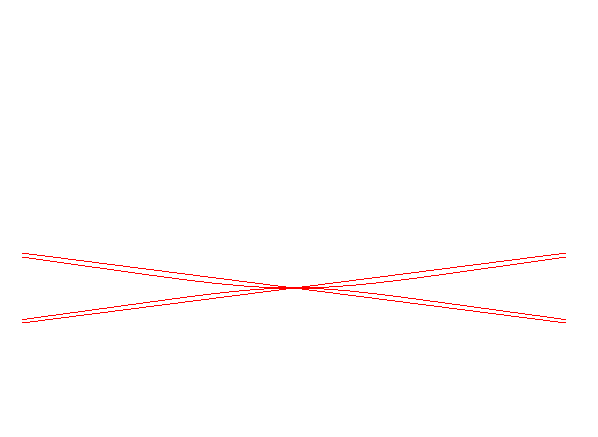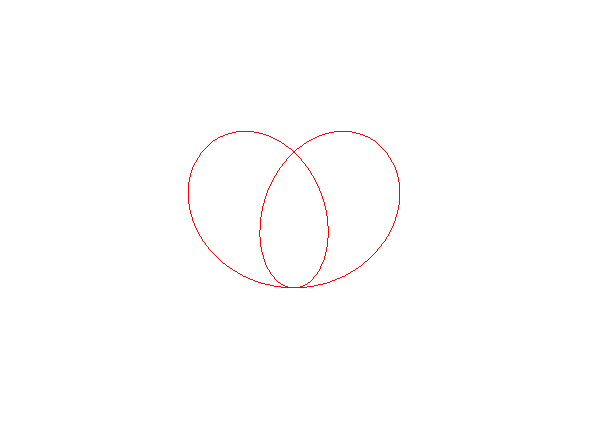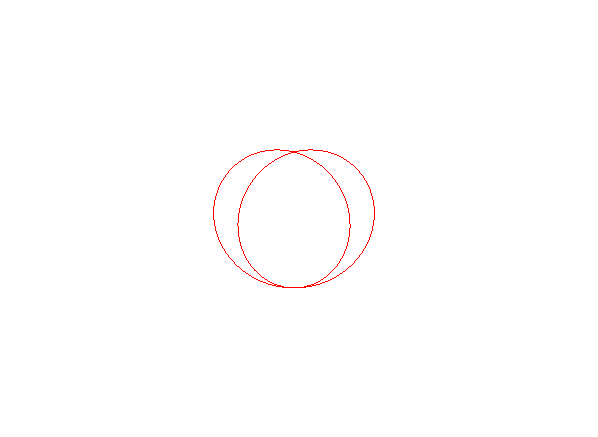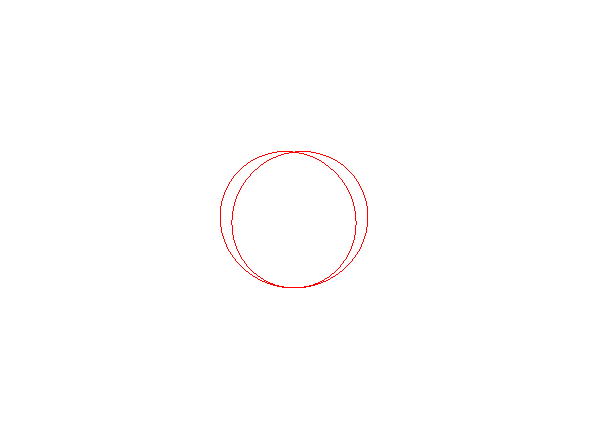
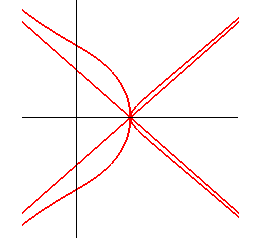
When A is outside the circle, there is a tacnodal double point and two asymptotes.

Besides, these two cases are inverses of one another: more precisely, the curves  and  are inverses of one another with respect to the circle (C).

Writing the polar equation  where e = 1/k, proves that the Jerabek curve is the conchoid of a centred conic with pole a focus of this conic, and modulus the semi-major axis (see conchoid of a conic).

It is also the pedal of the evolute of a centred conic with respect to one of its foci.
 
 

When A is inside the circle, if I is the middle of [MP] , IM = IP = IA, so OI + IA = OP = constant: the point I describes an ellipse and the Jerabek curve can be obtained by decreasing the radius vector of the green ellipse starting at the focus O by a length equal to the radius vector that reaches the other focus A. Let J be the image of I by the homothety with centre O and ratio 2; J describes the blue ellipse and JM = OP = constant: the Jerabek curve is the conchoid of the blue ellipse with respect to the focus O, the radius vector being decreased by the semi-major axis of this ellipse. M is the symmetrical image of A with respect to the normal to the green ellipse passing by I: the Jerabek curve is therefore the orthotomic with pole A of the involute of the evolute of the green ellipse. See strophoidal curves, for a strophoidal construction of the Jerabek curve using this property.

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL 2017