Kiepert curve

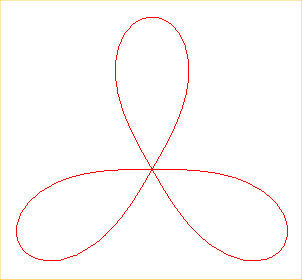
KIEPERT CURVE

Curve studied by W. Roberts and L. Kiepert in 1870.
Friedrich Wilhelm August Ludwig Kiepert (1846-1934): German mathematician.
Other name of this curve: lemniscate with three poles.

Tripolar equation:

where (ABC) is the equilateral triangle A(d), B(dj), C(dj²).
Polar equation:

with

.
Cartesian equation:

.
Tricircular sextic of genus 1.

The Kiepert curve is the sinusoidal spiral of order 3, it is therefore a special case of Cassinian curve; it is to the equilateral triangle what the lemniscate of Bernoulli is to the bipoint.

Its inverse with centre O is the Humbert cubic.

Compare to the regular trifolium.

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra