LIMAÇON (OR SNAIL) OF PASCAL
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
LIMAÇON (OR SNAIL) OF PASCAL

| Curve studied by Dürer in 1525 (under the name Arachne),
Etienne Pascal in 1630, and Roberval (who named the curve) in 1650.
Étienne Pascal (1588 -1651): magistrate and amateur mathematician, father of Blaise. |
| Polar equation: Complex parametrization: Cartesian equation: Rational bicircular quartic (singular point at O). Area for e |
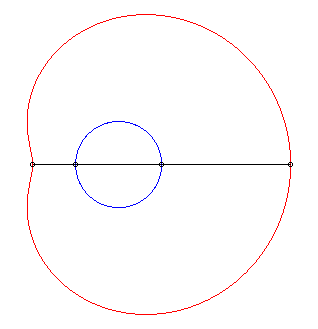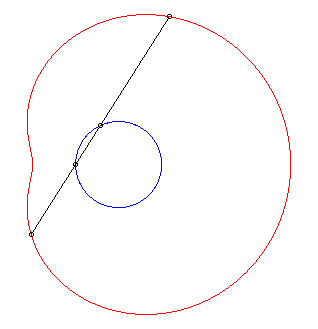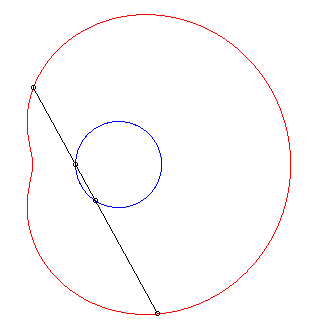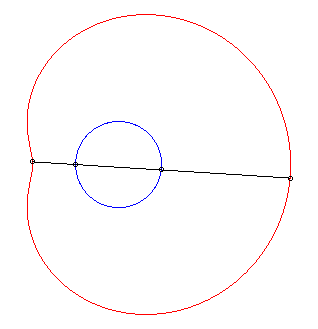
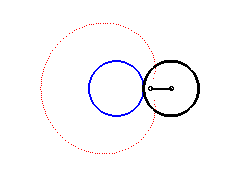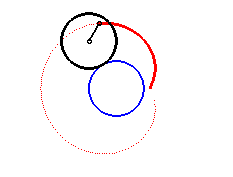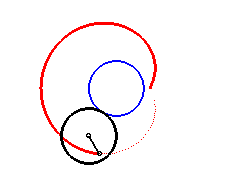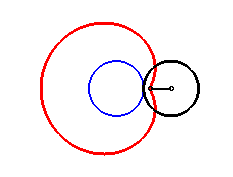
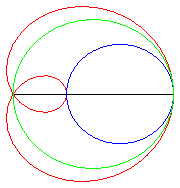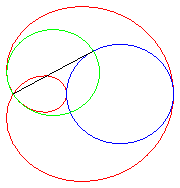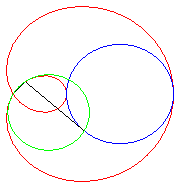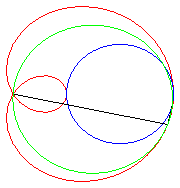
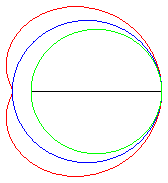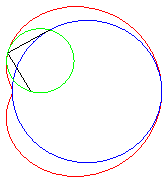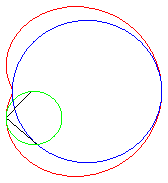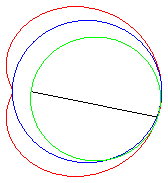
| The limaçons of Pascal are the conchoids
of a circle with respect to one of its points O (here, the circle
with diameter [OA] with A(ea, 0)).
Hence the mechanical construction suggested opposite, thanks to a stick of length 2a sliding through a point of a circle with diameter ea and the middle of which is constrained to describe the circle. |
 |
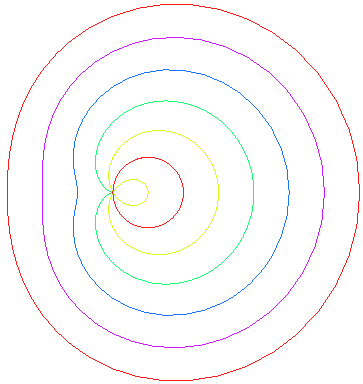
The curves assume different shapes depending on the cases:
| e < 1: elliptic limaçon (inverse
of an ellipse with respect to its focus), or with an isolated point,
or acnodal;
.e < 1/2: convex curve that "tends" to the circle C(O,a) when e goes to 0. .e = 1/2: limaçon of Pascal with a meplat. .1/2 < e < 1: curve with the shape of a bean; e = 1: cuspidal limaçon more commonly called cardioid. e > 1: hyperbolic limaçon (inverse of a hyperbola with respect to its focus) or with a loop, or crunodal; it is a closed curve with a loop; for e = 2, we get the trisectrix limaçon, which is also a rose. |
 |
The complex parametrization above shows that the limaçons of Pascal are the epitrochoids generated by a point linked to a circle rolling without slipping around a circle with the same radius (here the fixed circle is the circle with diameter [OA] and the tracing point is located at distance a from the centre of the moving circle).
 |
 |
 |
 |
- the cissoids of two circles, one of which passes through the centre of the other, with respect to this centre (here, cissoid with respect to O of the circle with centre (-ea/2, 0) passing by O and the circle with centre O and radius a - this definition is in fact equivalent to the conchoidal definition).
The limaçons of Pascal are the rational Cartesian
curves and are special cases of complete
Cartesian ovals; when e1
(i.e. when it is not a cardioid), the bifocal equation with respect to
O
and O' (
,
0) is:
.
More precisely:
- the hyperbolic limaçon is the reunion
of two Cartesian ovals:
(big loop) and
(small loop).
- the elliptic limaçon is the Cartesian
oval:
(plus the isolated point O).
We also find the limaçons of Pascal in the Bélidor drawbridge system.
The evolutes of the limaçons are the caustics
by reflection of circles (light source at finite distance).
 |

The Arachnes... |
The curves with equation |
See here a gear shaped like a limaçon of Pascal, and on this site a technical application to the "24 hour clock".
See also the general conchoids of circles.

Image made by par Daniel Alexis
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017