| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
GOLDEN SPIRAL, FIBONACCI SPIRAL
and natural spirals
|
|
|
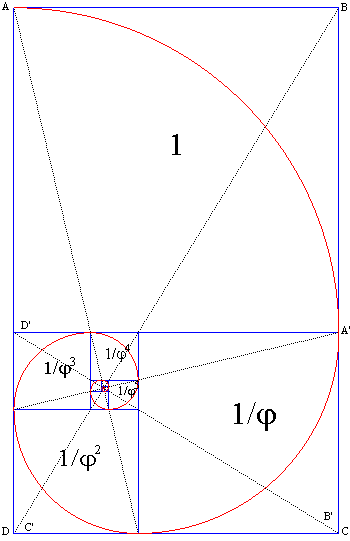
The figure starts with a golden rectangle ABCD,
with AB = 1 and 
= the golden ratio;
we draw the square ABA'D' and get the golden rectangle
A'B'C'D'
the length of the sides of which are 
and 1.
This process is repeated to get the rectangle A''B''C''D'' and so on and so forth, as well as the external squares; the golden spiral is composed of consecutive quarters of circles inscribed in each square. The dotted diagonals BD and CD' intersect at the point O, which is the asymptotic point of the spiral, called "eye of God" (the golden ratio being also called the "divine proportion"!) The lines AA'' and A'A''' are perpendicular and intersect at O. |
 |
The golden spiral possesses a partial "eadem mutata resurgo"
property, namely it is invariant under similarity with centre O,
ratio 
and angle  ;
therefore, it approximates a true logarithmic spiral where m is defined by  ,
hence
with polar equation ,
passing by the points A, A', A" etc...
With each turn, the
radius of the golden spiral is multiplied by
|
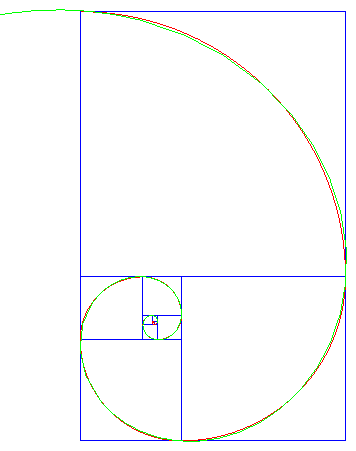
The golden spiral (in red) and the true logarithmic spiral (in green) |
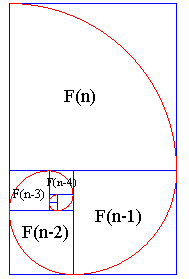
| If, instead of starting from a golden rectangle, we begin with a Fibonacci rectangle, with AB = Fn-1 and BC = Fn, where Fn-1 and Fn are two consecutive Fibonacci numbers, we get a spiral composed of quarter of circles called Fibonacci spiral which approximates the golden spiral, but does not have the "eadem mutata resurgo" property. |
  |
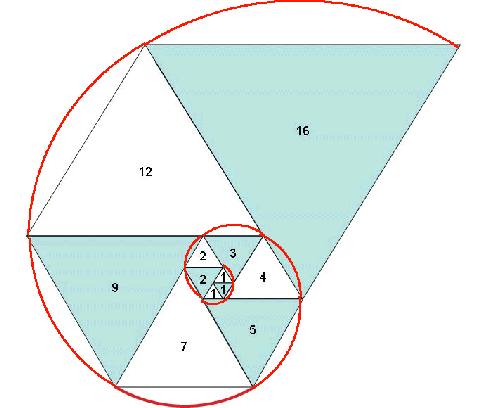
We can also begin with a golden triangle (isosceles triangle
with angle at the vertex equal to  ).
We get a spiral that can be called triangular golden spiral; when
this spiral is turned by  ,
it is enlarged by a factor j ; therefore, it
is an approximation of the logarithmic spiral  ;
the enlargement factor at each turn is 
and the polar tangential angle is about 76°. |
 |
| See also the Padovan spiral, the enlargement factor at each turn of which is the sixth power of the Padovan number, i.e. about 5.4. |
 |
| On this site, can be found an explanation of the fact that the shell of the nautilus supposedly approximates a golden spiral, but this is obviously contradicted by a direct observation: the spiral of the nautilus is much tighter and experimental measurements show that its enlargement factor is about 3 which is clearly less than the 6.9 of the golden spiral... |  |
 Ammonite: clearly smaller enlargement factor.... |
 The tendril of the green bean supposedly approximates the triangular golden spiral... |
 |
Compare the construction of the golden spiral to that
of the spiral with n
centres, which approximates an Archimedean spiral.
Swiss stamp from 1987
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017
;
the constant polar tangential angle is equal to 