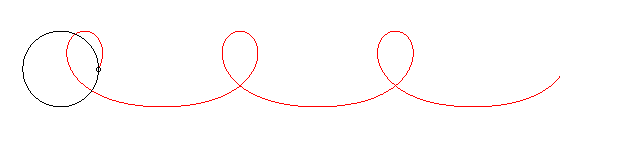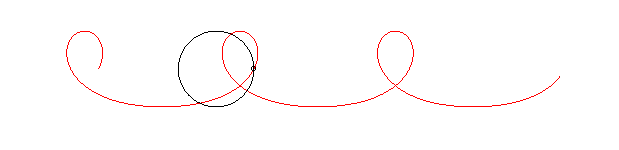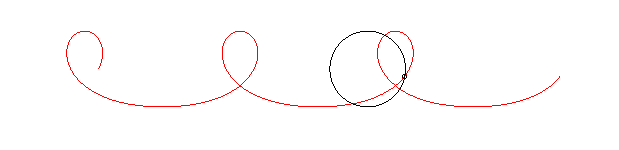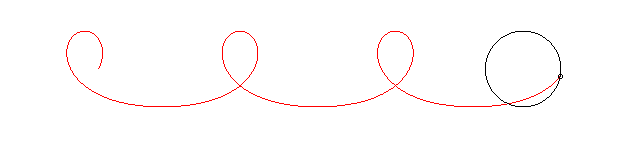
The name "Mascot curve" comes from the fact that the circle can represent the edges of a regiment, and the point M a dog, mascot of the regiment, turning around the regiment at constant speed.

This problem is a variation on a problem posed by Martin Gardner in 1960 (under the name "marching cadets and a trotting dog") in the Scientific American journal in the case of a square regiment.

We can also consider that it is the curve described by a ship turning around another ship while maintaining a constant distance between them.
 

If  and V are the respective speeds of the regiment and the mascot, R the radius of the circle, and  the angle locating the mascot on the circle, then the kinetic equations of motion are given by: , being defined, for a mascot turning counter-clockwise, by the differential equation: where  and . Cartesian parametrization of the trajectory: . Distance travelled by the mascot when it completes one turn of the regiment: ( elliptic function of the second kind) i.e.  when the mascot goes twice as fast as the regiment (k = 2).

The mascot curve looks like a trochoid with a loop, but isn't one: the trochoid would correspond to the case where the speed of the mascot is constant with respect to the regiment instead of the floor.

In the example below where the mascot goes 1.5 times as fast as the regiment, notice the widening of the curve between the two loops:

© Robert FERRÉOL  2017