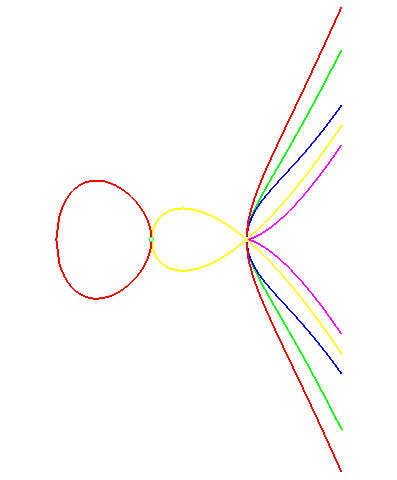
green: acnodal cubic
blue: elliptic cubic with a branch
yellow: crunodal cubic
magenta: cuspidal cubic
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
DIVERGENT PARABOLA
 |
red: elliptic cubic with an oval
green: acnodal cubic blue: elliptic cubic with a branch yellow: crunodal cubic magenta: cuspidal cubic |
| Curve studied by Newton in 1701. |
| Cartesian equation: Cubic. |
The divergent parabolas are the curves defined by the above Cartesian equation.
Any cubic is projectively equivalent to (i.e. is the image by a real homographic transformation of) a divergent parabola (Newton theorem). Since all homographies are composed of a direct isometry and a homology (or perspective), this means that any cubic can be seen under a certain perspective as a right divergent parabola.
Therefore, the cubic is rational if and only if the discriminant
D
of the polynomial P above is equal to 0, and, in this case, there
are three projective equivalence classes, composed of the crunodal,
acnodal and cuspidal cubics.
In the non-rational case (cubic of genus 1, called "elliptic
cubic"), every value of D gives a projective
equivalence class.
| Arrangement of the zeros of P | Type of the cubic |
| Three distinct real zeros;
reduced equation: |
Elliptic cubic with an oval |
| A real zero and two conjugate complex zeros;
reduced equation: |
Elliptic cubic with a branch |
| Two real zeros, one of which has multiplicity 2, and
P(x)
³
0 in a neighbourhood of the double root;
Reduced Cartesian equation: Cartesian parametrization: Therefore, the cubic is polynomial. This case includes the Tschirnhausen cubic: (b = 3 a), the right parabolic folium (b = a) and a case of Lissajous curve (a = 3 b). |
Crunodal cubic (with double point) |
| Two real zeros, one of which has multiplicity 2, and
P(x)
£
0 in the neighbourhood of the double root;
Reduced equation Cartesian parametrization: Polynomial cubic. This case includes the duplicatrix cubic (b = a). |
Acnodal cubic (with an isolated point) |
| A triple real zero: semicubical parabola. | Cuspidal cubic (with a cuspidal point) |
In the last three cases, the divergent parabola can be obtained by antihyperbolism of the parabola (hence the name divergent parabola).
See also the Chasles
cubics, the cubical
hyperbolas (other families of curves representing all cubics), the
pursuit
curves, and the swimming dog curve.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017