POINSOT SPIRAL

| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
POINSOT SPIRAL


| Curve determined by Cotes in 1722.
Louis Poinsot (1777 - 1859): French mathematician. Other names, along with the epispirals: Cotes spiral. |
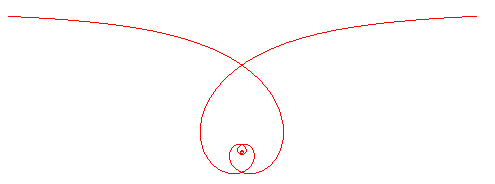
The Poinsot spiral is the curve with
| Polar equation: |
When
-
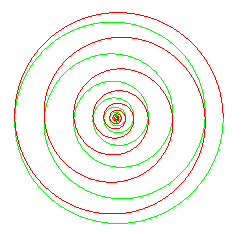
we get a logarithmic spiral
-
we get a bounded spiral similar to
.
- we get a spiral with asymptote similar to
.
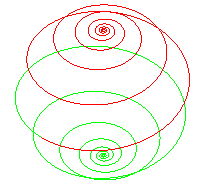
| The bounded Poinsot spiral is the orthogonal projection on the equatorial plane of the rhumb line of the sphere |
  |
|
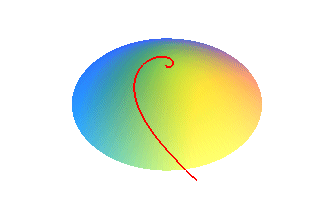
The Poinsot spiral with an asymptote is the projection of the curve traced on a hyperboloid of two sheets |
 |
The Poinsot spirals are solutions to the problem consisting in determining the trajectories in space of a massive point subject to a force centred on O proportional to (this force is, according to the Binet formula, proportional to
which is equal, here, to
, with
); the other solutions are the epispirals with, as an intermediary case, the hyperbolic spiral, see this link.
The trajectories of a marble thrown in a tube and in uniform rotation are the inverses of the bounded Poinsot spirals (Jean Bernoulli, Opera, T IV, p 248).
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017