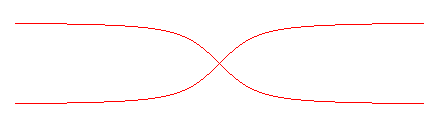
Bullet nose curve

BULLET NOSE CURVE

Curve studied by Pieter Schoute in 1883.

Cartesian equation:

(special case of Lamé curve), or

or also

.
Cartesian parametrization:

.
Rational quartic.
Area between the curve and the asymptotes: 4ab.

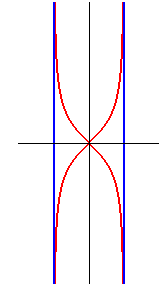
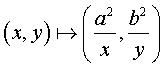
The bullet nose curve is the image of the hyperbola (here ) by a biaxial inversion (axes those of the hyperbola), defined by: ; geometrically, it is the locus of the intersection points between a tangent to the hyperbola and the axes.

The bullet nose curve is therefore to the hyperbola what the cross curve is to the ellipse.

Do not mistake for the kappa.

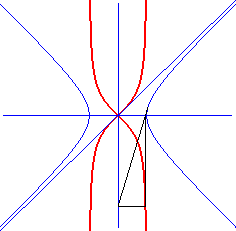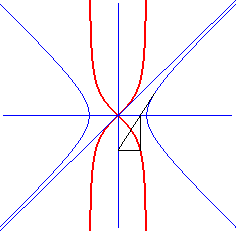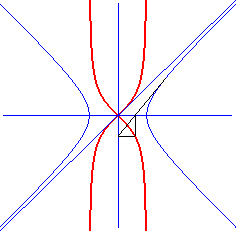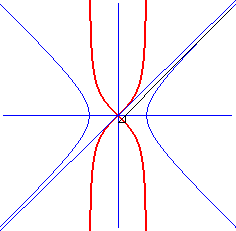
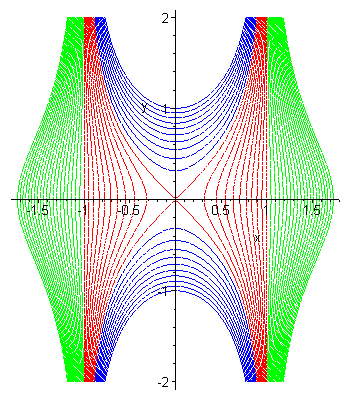
Opposite, the family of quartics with equation , which are no longer rational (in green for k < 0, in red for and in blue for k > 1).
The bullet nose curve is obtained for k = 1 (limit between the blue and red curves).

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra