Crawl curve

Reptoria

Curve studied by Jean Bernoulli in 1742 (who gave it the Latin name of reptoria) and by Prouhet in 1854.

If the base is parametrized by (M(t)) and the crawling curve is parametrized by (N(u)), then the reptoria is parametrized by (M(t)-N(u)), with the parameters u and t linked by

When a moving curve (the crawling curve) has a translation motion such that it remains tangent to a fixed curve (the base), the curves traced by a point of the plane of the moving curve on the fixed plane are called reptorias.

Properties:
    1) the tangent to the reptoria is parallel to the common tangent to the base and the crawling curve at the contact point.
    2) the various reptorias are all translated images of each other.
    3) if the base and the crawling curve are swapped (but their orientation isn't changed), the new reptorias are the images of the previous ones by point reflection.
    4) if a reptoria now crawls on the base, the new reptorias are the translated images of the previous crawling curve.
    5) when a circle with radius a crawls on a curve, the reptoria of the centre of the circle is one of the 2 parallel curves at distance a (ditto if the curve crawls on the circle).
    5) if the reptoria and the crawling curve are given, the base can be obtained as the envelope of the various positions of the crawling curve.

Nota 1: the base defined here is different from the base in the sense of the motion of a plane over a fixed plane, which is at infinity in this case.
Nota 2: in a more modern language, the properties 2 and 3 can be expressed as: if F₁, F₂ and F₃ are three parametrized curves with zero sum and derivatives pairwise collinear, and {1,2,3}={i,j,k} then, if Fj crawls on - Fi then the reptoria is Fk.

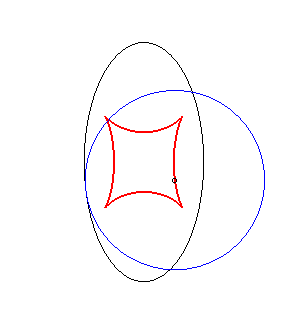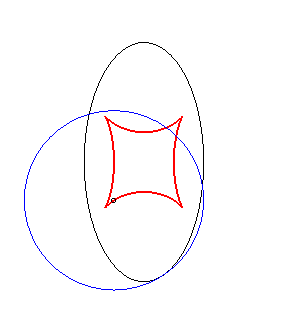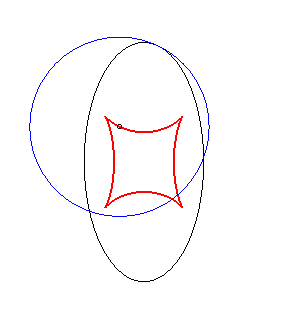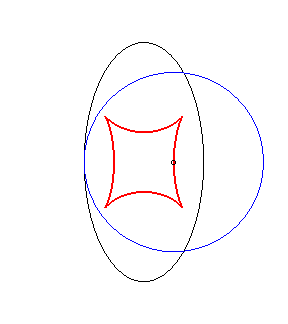
Example illustrating this last property (base in black, crawling curve in blue and reptoria in red):

,

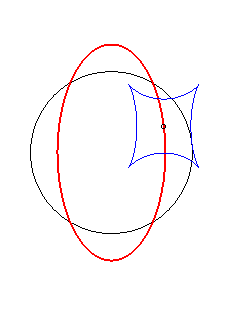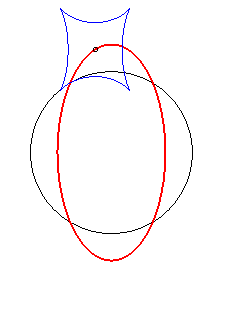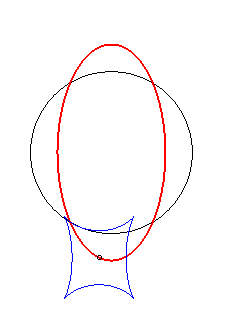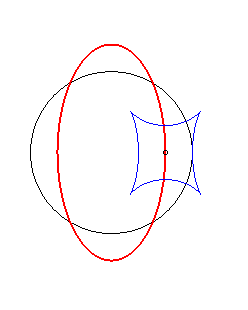An ellipse (E) crawls on circle (C): we get a reptoria (R) (C) crawls on (E): we get the same reptoria, which thus is a curve parallel to the ellipse (or toroid) (R) crawls on (C): the reptoria is the ellipse (E)

(R) crawls on (E): the reptoria is the circle (C)

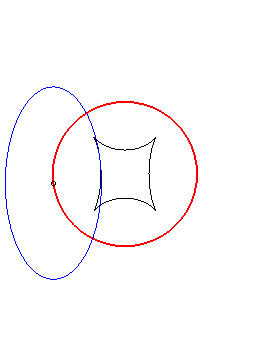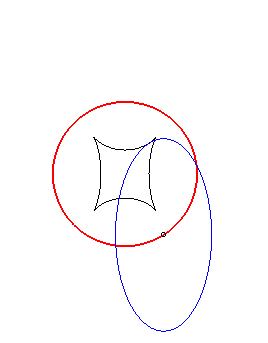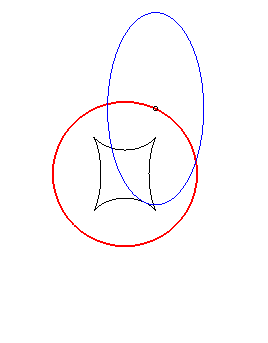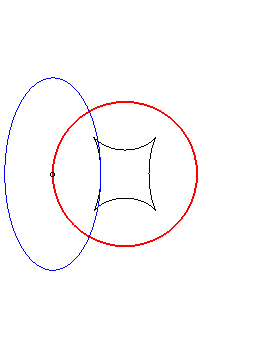
(E) crawls on (R): the reptoria is the circle (C)

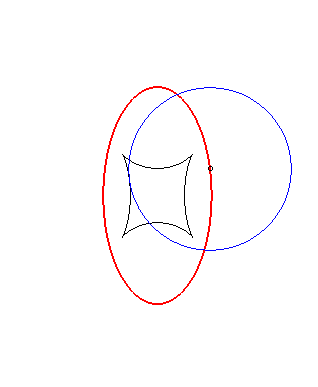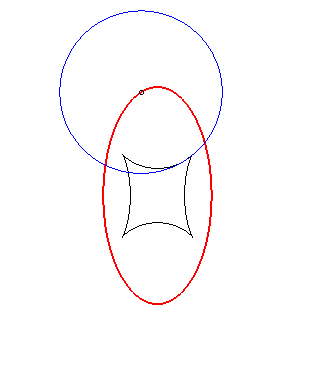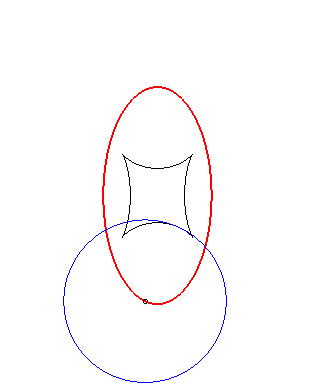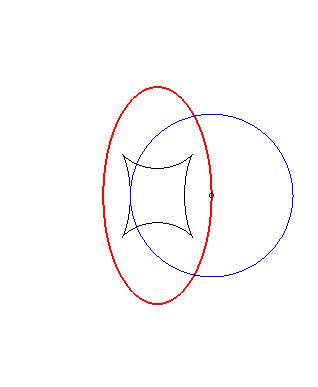
(C) crawls on (R): the reptoria is the ellipse (E)

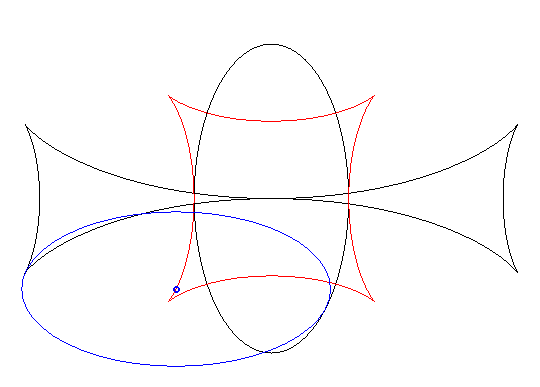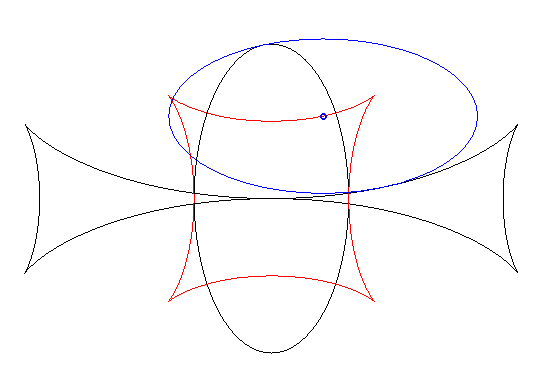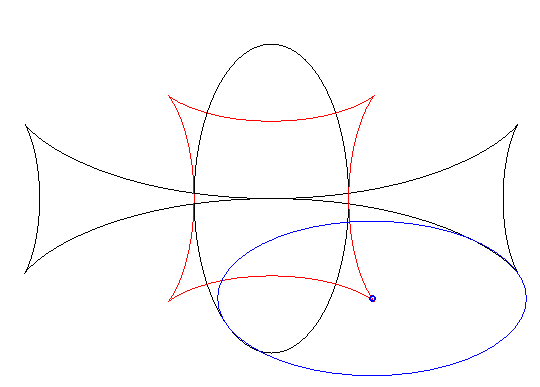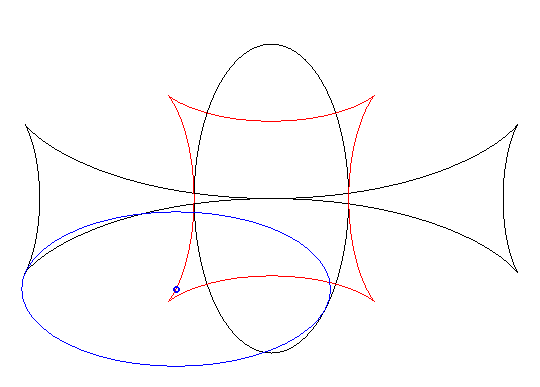
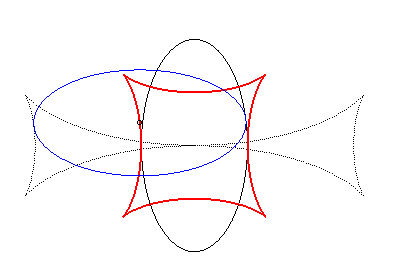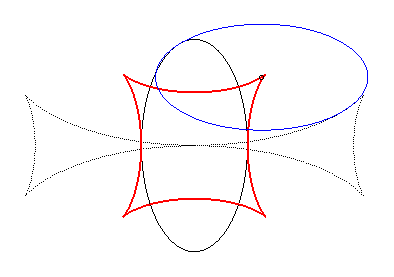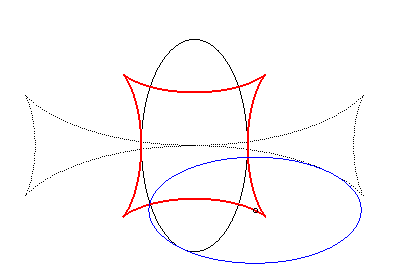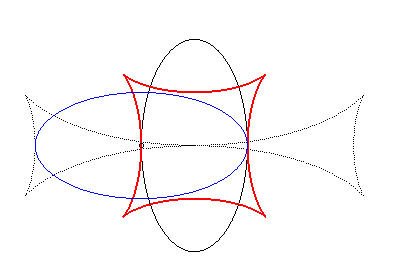
When an ellipse crawls on its image by a 90° rotation, its reptoria is a curve invariant under 90° rotation similar to the astroid (but not rational), parametrized by:
The crawling curve envelopes another curve (in dotted line opposite), similar to the Maltese cross when b = 2a.