Notion studied by Besant in 1869.

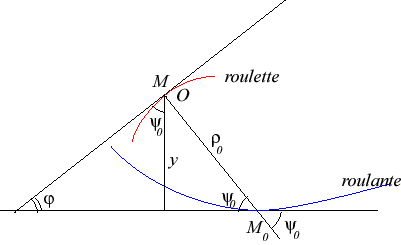
Given a curve () and a point O linked to (), the associated roulette with linear base is the trace of the point O when the curve () rolls without slipping on a fixed line. Therefore, this is a movement of a plane over a fixed plane the base of which is linear.
 
 

The formulas linking the equations of the rolling curve () and of the roulette () are . Starting from a rolling curve , we get the roulette . Conversely, starting from a roulette , we get the rolling curve , the pedal of which can be obtained more simply by the formulas: . The curvilinear abscissa and the radius of curvature of the rolling curve are given by: In complex parametrization, the relation can be written: .

Examples:
 

figure	rolling curve	tracing point	roulette
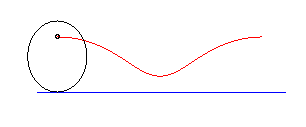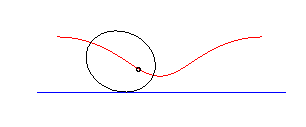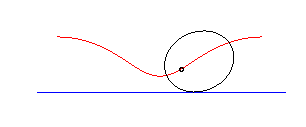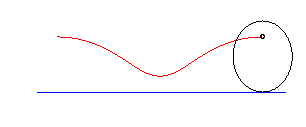
	circle	on the circle	cycloid
	circle	outside the circle	trochoid
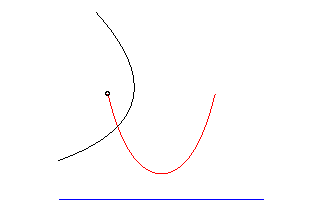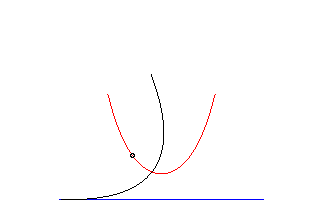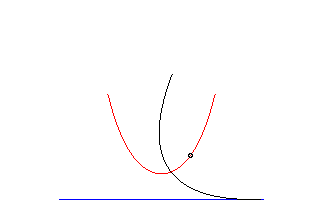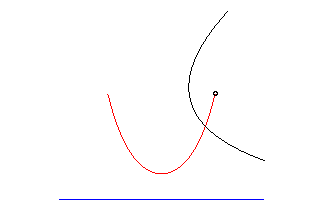	parabola	focus of the parabola	catenary
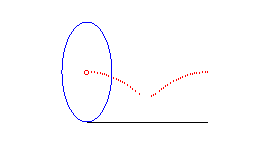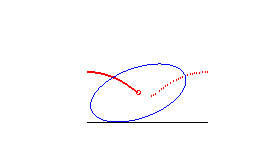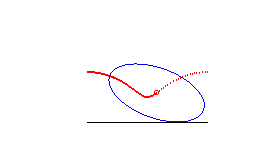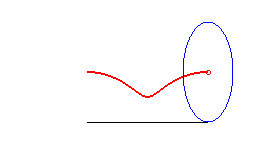
	centred conic	focus of the conic	Delaunay roulette
	centred conic	centre of the conic	Sturm roulette
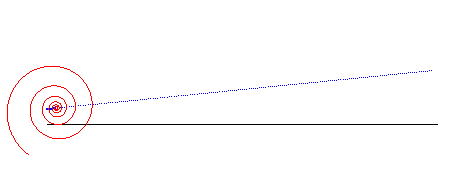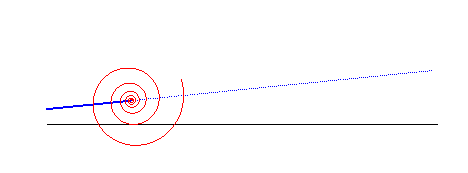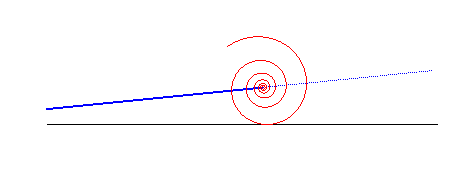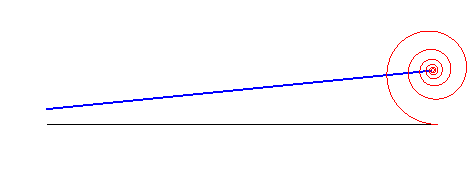	logarithmic spiral	centre of the spiral	line
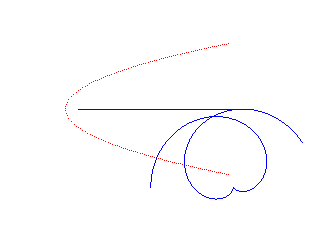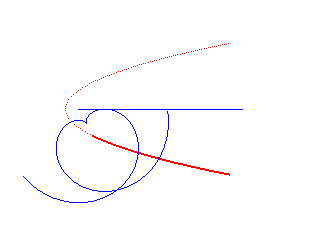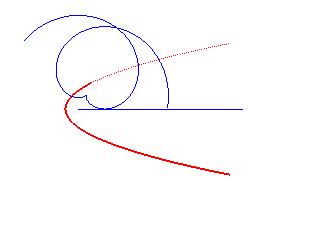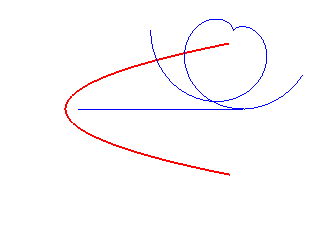	involute of a circle	centre of the circle	parabola the base of which is the symmetry axis
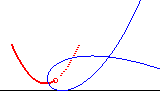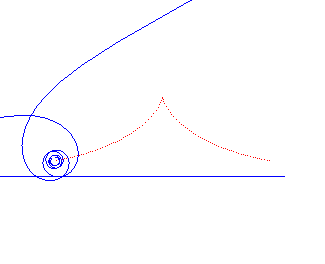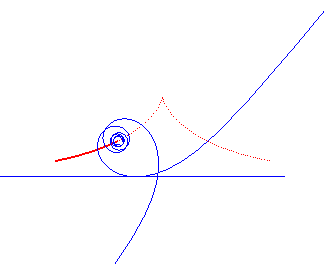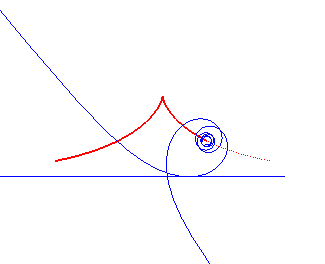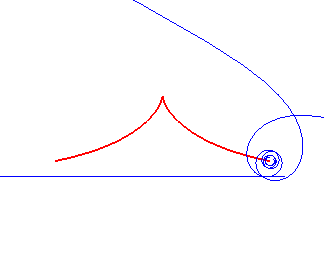
	Tschirnhausen cubic	focus of the cubic	parabola the directrix of which is the base of the rolling motion
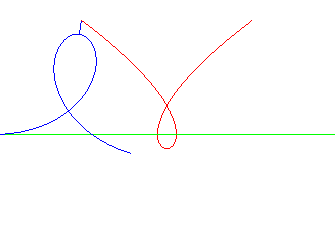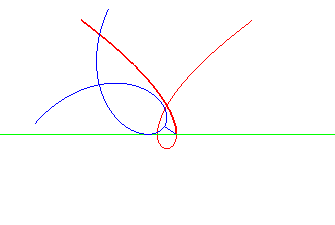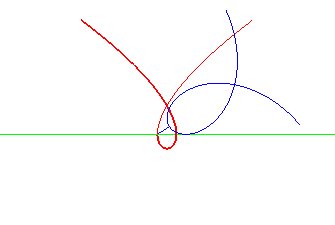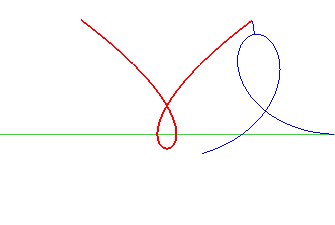	Norwich spiral	pole of the spiral	Tschirnhausen cubic
	hyperbolic spiral	centre of the spiral	tractrix
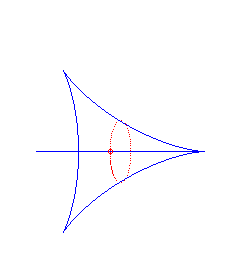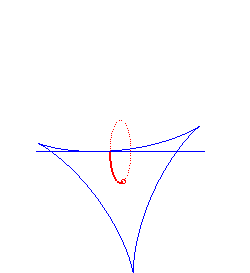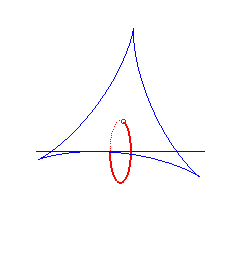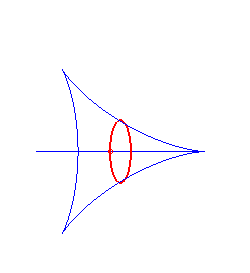	centred cycloid	centre of the cycloid	ellipse
	sinusoidal spiral of index n	pole of the spiral	Ribaucour curve of index 1+1/n

Since the roulettes with linear base of a curve are identical to the glissettes with linear base of any involute of this curve, see other examples at glissette.

Compare to the notion of wheel-road couple, where, now, it is the roulette that is linear instead of the base.
 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2017