Cartesian equation: , a, b > 0 , or . Cartesian parametrization: 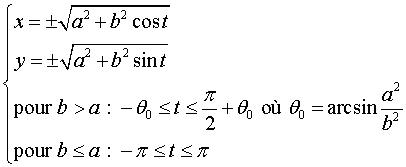. Quartic of genus 3 when b is different from a and from , decomposed quartic when b = a, and of genus 2 for b = .

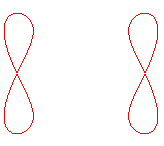
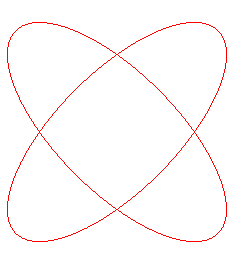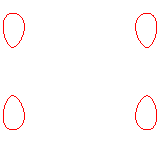
For b = a , the quartic can be decomposed in two ellipses (cf the second equation)		For b < a, it is composed of 4 connected components surrounding the vertices of a square (with coordinates ), which is the maximum possible for a quartic.
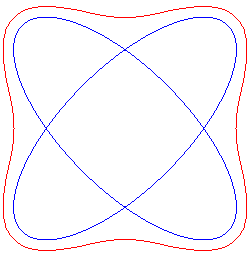
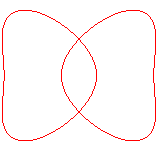
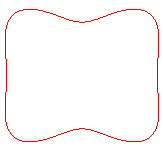
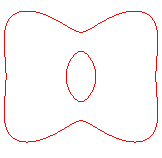
For a < b < , it is composed of 2 connected components, with the central component degenerating into an isolated point for b = . The quartic is said to be "ring-shaped".		For b > , there is only one component left.
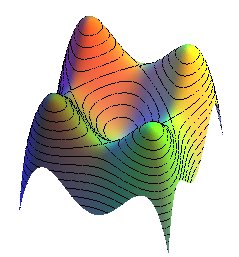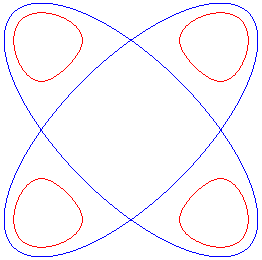
All this can be easily seen on the surface  the contour lines of which are the Salmon quartic.		For 0 < b < a, the Salmon quartic has, visually, 4 times 6 = 24 bitangents, like 4 circles would.	Salmon quartic and 6 of its 24 bitangents
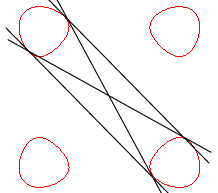For , the 4 connected components have a concave part and therefore have one bitangent each. The Salmon quartic has, in this case, 24+4=28 real bitangents, the maximum possible for a quartic.	The 4 additional bitangents in that case.	Yet, a quartic can only have 28, 16, or at most 8 real bitangents. Where are the four missing bitangents in the case where the 4 components are convex? They indeed are real (in blue opposite), but their tangency points with the quartic have complex coordinates!

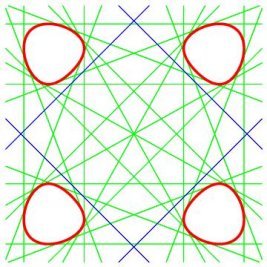To obtain the same phenomenon of the 4 components and the 28 bitangents, we can cross ellipses in order to emphasize the concavity of the "meniscus". Opposite, the curve  for b=0.3a and k=0.01, with its two directrix ellipses, and its 28 bitangents. (Cf. the Trott curve).

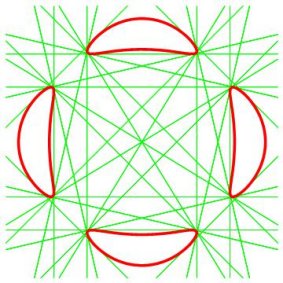Cf. also the Plücker quartic, which is the historical example of a quartic with 28 bitangents.
 

Salmon studied, more generally, the quartic  the different shapes of which indicated below are visible on the plot of the surface  opposite.

b < a1 < a2	b=a1<a2	a1 < b < a2	a1 < a2 = b	a1<a2<b<(a1^4+a2^4)^(1/4)	a1<a2<(a1^4+a2^4)^(1/4)<=b

 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL 2017