Rational sextic

RATIONAL SEXTIC

The rational sextics are the sextics of genus zero, therefore with between one or ten singularities making the genus decrease by 10 (in the complex projective plane).

Cartesian parametrization: where P, Q and R are three polynomials with real coefficients the maximum of the degrees of which is 6.
Replacing t by , we get a trigonometric parametrization: .

Most of the remarkable rational sextics are part of the family of the rational curves of degree 6 that are bounded, with Oy as a symmetry axis, and parametrization , as it will be noted thereafter.

Examples of rational sextics:
    - the quadrifolium and its conchoids: (a = 0: quadrifolium, a = 1 : Ceva trisectrix , a = 2: double egg: a > 2: peanut curve)
     - the Dürer folium and its conchoids: (a = 0: Dürer folium, a = 1: Freeth's nephroid )
     - the epitrochoids with parameter q = 2:   (a = 1 : Dürer folium, a = 3: nephroid).
    - the hypotrochoids with parameter q = 4: (a = 1: quadrifolium, a = 3: astroid).
    - the epitrochoids with parameter q = 1/2: .
    - the hypotrochoids with parameter q = 5/2 (5-branch star): .
    - the cornoid:
    - the Maltese cross:
    - the double drop of water: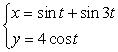
    - the Cayley sextic:
    - the Lissajous curve:
    - the windmill:
    - the bow tie curve:
    - the beetle curves: (including the quadrifolium: )
    - the Talbot curves: .

Here, an animated view of the sub-family with one parameter:
In order of apparition:
a = 0: quadrifolium
a = pi/4: Maltese cross
a= pi/2: double drop of water
a = 3pi/4: double egg
a = pi-arctan(1/2): Dürer folium
a= pi-arctan(1/3): curve similar to the cornoid
This curves are the projections on the planes containing Oy of the 3D curve:

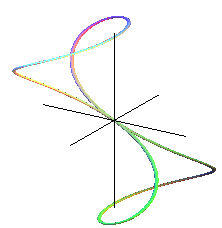Other examples:

A beautiful sextic with a triple point where the tangents coincide, which belongs to the family of the basins:

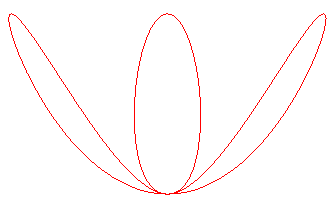Another one, which cannot be decomposed, though it seems to be composed of a circle and an eight: .

This third one also seems to be composed of a circle and a cardioid:
.
This curve is associated to the triangles an altitude, a median, and a bisector of which are concurrent (triangles considered by E. LEMOINE in 1885 in mathesis): if the vertex of the altitude is fixed on (0,1) and that of the median on (0,0), then this curve is the locus of the third vertex of such a triangle.
The locus of the intersection point is a septic.

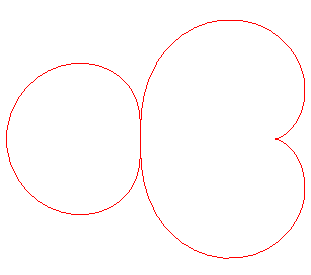next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

A beautiful sextic with a triple point where the tangents coincide, which belongs to the family of the basins:
Another one, which cannot be decomposed, though it seems to be composed of a circle and an eight: .
This third one also seems to be composed of a circle and a cardioid: . This curve is associated to the triangles an altitude, a median, and a bisector of which are concurrent (triangles considered by E. LEMOINE in 1885 in mathesis): if the vertex of the altitude is fixed on (0,1) and that of the median on (0,0), then this curve is the locus of the third vertex of such a triangle. The locus of the intersection point is a septic.