SPIRIC OF PERSEUS
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
SPIRIC OF PERSEUS
| Perseus, 2nd century BC: Greek scholar. |
Reduced Cartesian equation: 
with A > B, i.e.  .
Bicircular quartic, rational if C = 0, having real points only if  .
Polar equation:  . |
The spirics of Perseus
are the bicircular
quartics with a symmetry centre. Therefore, they are the cyclic
curves with respect to a centred conic, the deferent (corresponding
to the "initial curve" in the link) of which is this conic.
In other words, they are the envelopes of the circles the centres of which
describe a centred conic, and such that the centre of the conic has a constant
power with respect to these circles.
|
Case 0 < B < A fixed, C varying from minus infinity to A2 , case of the crossed torus. For  ,
curves are oval (in yellow),
for C = 0 , Booth oval (violet), with isolated point in the center, for  ,
two-component curves, a bean and an oval (in blue),
for  ,
union of circles of centers  ,
of radius  ,
for  ,
the curves, although real, no longer correspond to sections of a real torus,
for  ,
curves with two non-convex components (green),
for  ,
curves with two convex components (cyan),
for  ,
curves reduced to two points . |
 |
|
Case -A < B < 0 < A fixed, C varying from minus infinity to A2 , case of the open torus Pour ,
the curves have oval then bean shapes (yellow curves),
pour C = 0, Booth oval (violet), pour ,
two-component curves (in blue),
pour ,
union of circles of centers ,
of radius ,
pour ,
the curves, although real, no longer correspond to sections of a real torus,
pour  ,
curves with two non-convex components (green),
pour ,
curves reduced to two points . |
 |
Historically, these curves were defined as the sections
of a torus by a plane parallel
to its axis; but to obtain all the real curves given above, one has to
consider complex tori.
For a torus with centre O, axis Oz, with
major and minor radii a and b, cut by the plane parallel
to Oz located at distance d from O, we get, in a frame
with origin the projection of O on this plane, the Cartesian equation
above with: 
.
This comes from the equation: 
of these curves.
Note that the torus above is real only if 
.
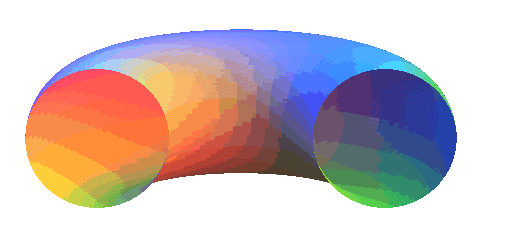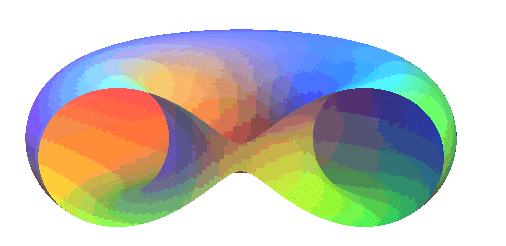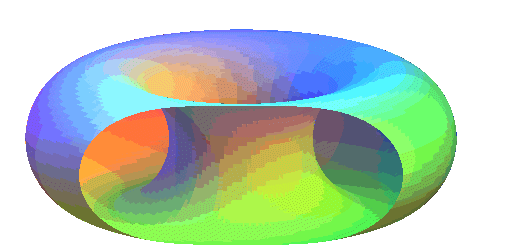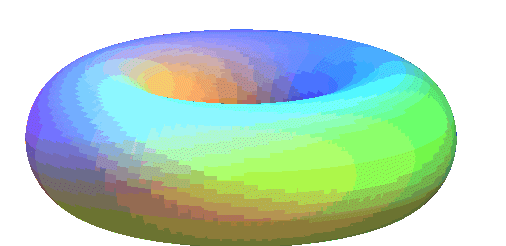
Spirics of Perseus of a ring torus |
|
When 
,
i.e. d = b (distance of the plane to the axis equal
to the minor radius), we get the Cassinian
ovals, which reduce to the lemniscate
of Bernoulli when C = 0, i.e. a = 2 b.
When C = 0, i.e. 
(plane tangent inside the torus), we get the Booth
curves (or Hippopedes of Proclus), which also reduce to the lemniscate
of Bernoulli when a = 2 b.
The limit case A = B (case where the torus is reduced to a sphere) gives circles.
The spirics of Perseus are also the isoptic curves of the centred conics.
Les courbes d'équation tripolaire où
O est le milieu de [FF'] forment une sous-famille à
un paramètre des spiriques de Persée.
En effet dans le repère où et
ces courbes ont pour équation : , donc pour cette famille :
.
The tripolar equation curves 
where O is the midpoint of [FF'] form a one-parameter subfamily
of Perseus spirics.
Indeed in the reference where 
and 
these curves have the equation 
:
, therefore for this family:
.
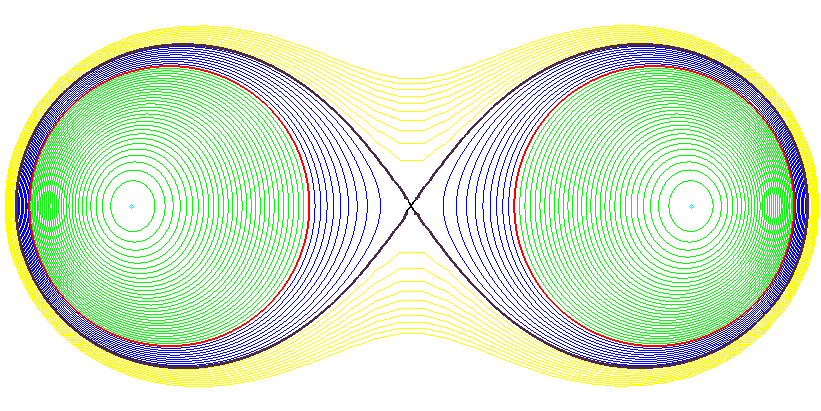
The curves only correspond to real torus sections for  .
For  ,
we get booth "focuses" F and F',
for  ,
two-component curves (green),
for  ,
non-convex two-component curves (red),
for k = 2, union of two circles of centers the focuses and radius  ,
for k > 2, two-component curves (cyan). |
 |
|
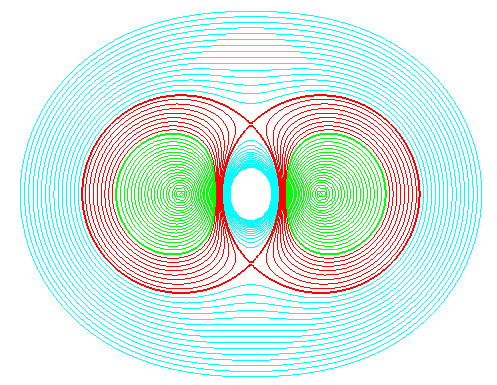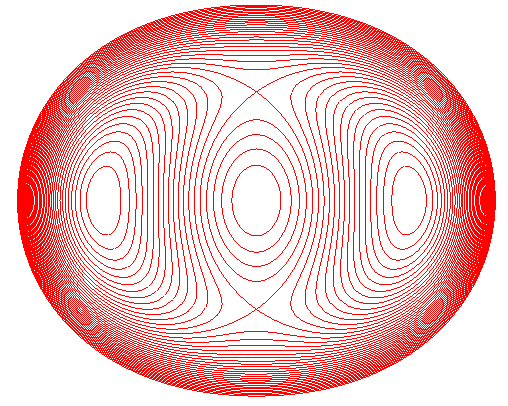
Disk composed of a birefringent diametrically charged material observed under polarised monochromatic light. The black lines - the isochromatic lines - are the loci of the points for which the difference of the 2 principal constraints is constant. Picture by Mr Konieczka and Ms Gautherin, Laboratory of Mechanics of the Department of Mechanical Engineering of École normale supérieure (ENS) de Cachan |
 |
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2024
