NORWICH SPIRAL
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
NORWICH SPIRAL
| Curve studied by Ricatti in 1712, Euler in 1781,
Sturm
in 1857, and Sylvester
in 1868.
The name of Norwich spiral was given by Sylvester in reference to where a congress was held in 1868 during which he presented his works about the consecutive involutes of a circle. Other names: Sturm spiral, radioid. Ref: [Loria] p.168. |
The Norwich spiral
is the curve, different from a circle, such that the radius of curvature
is, at all points, equal to the distance to a fixed point (hence the name
radioid).
It is therefore a special case of Sturm spiral.
Differential equation: 
(p is the pedal radius).
First integral:  ,
the case a = 0 gives the circle, but, in the case a > 0,
we get:
Polar equation:  ,
polar parametrization:  .
Curvilinear abscissa:  ,
polar tangential angle:  .
Pedal radius:  ,
radius of curvature:  .
Intrinsic equation 1:  . |
 |
| On the right, figure illustrating the fact that any point
on the Norwich spiral (in red) is at the same distance from the centre
of curvature as from O.
In blue, the evolute, locus of the centres of curvature. |
 |
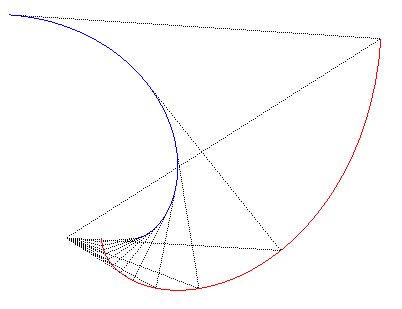| It can be noticed, during, for example, the derivation
of the intrinsic equation, that this evolute is none other than an involute
of a circle (more precisely, of the circle with centre O and
radius 2a).
The Norwich spiral is therefore one of the second involutes of a circle. And the second involutes of a circle are the curves such
that the radius of curvature is, at all points, equal to the distance to
the centre of the circle, plus a constant.
|
 |
The Norwich spiral is the negative
pedal of the Galilean spiral:  , |
 |
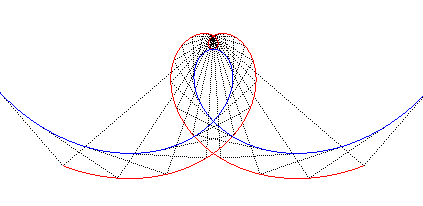and it is asymptotic to the Galilean
spiral : . |
 |
See also the links between the Norwich spiral and the
Tschirnhausen
cubic, as well as the inverse Norwich
spiral.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017