Curve studied by Antonio Pita in 2008.

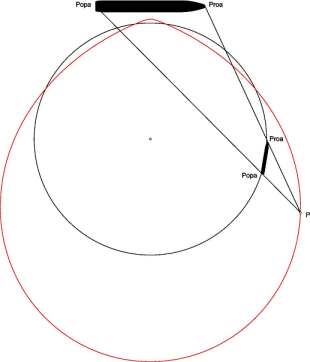
When two boats move in the plane, the associated superposition curve is the locus of the points of the plane from which the bows and the sterns of the two boats each seem to be on the same line.
More precisely, when two segment lines [AB] and [A'B'] with constant lengths move on the plane, the associated superposition curve is the locus of the intersection points between the lines [AA'] and [BB'].

Examples:
 

If one of the boats is fixed while the other is in translation, then the superposition curve is a hyperbola.

If one of the boats is fixed while the other is in rotation, then the superposition curve is a rational quartic. See also the case of the fish curve.

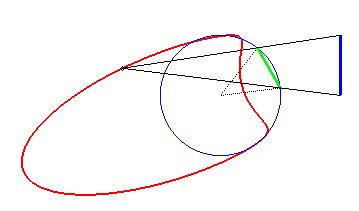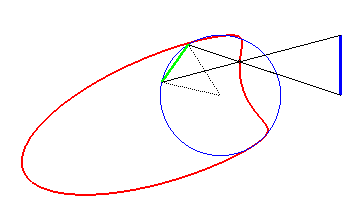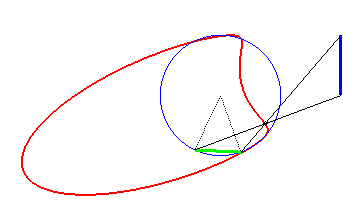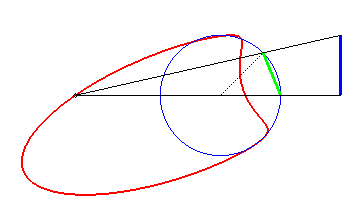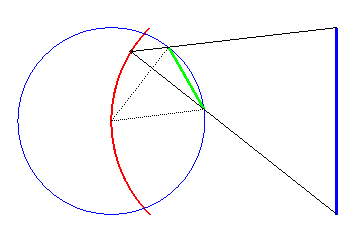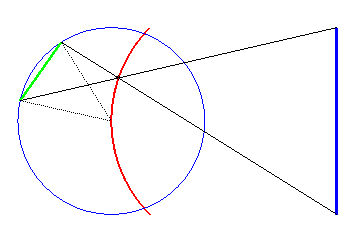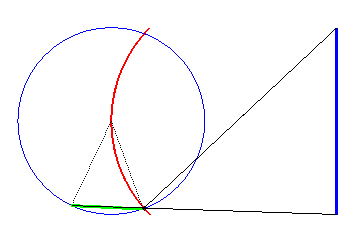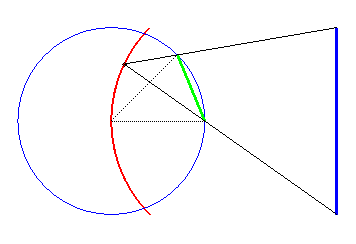
If the axis of the fixed boat [AB] passes through the centre O of the circle described by the moving boat and O is a point on the superposition curve, then the latter is an arc of the circle circumscribed to the triangle (OAB).

 

Closer to reality: case where the bow is tangent to the circle (realisation: Alain Esculier).

Here is an example of superposition where the two boats have circular motions, one going twice as fast as the other (realisation: Antonio Pita).

 

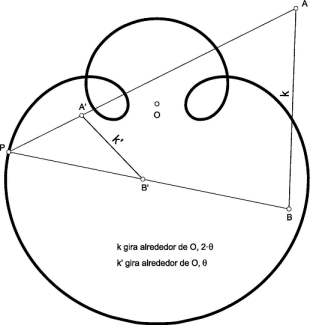next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2017