Symmetric image of a curve

SYMMETRIC IMAGE OF A CURVE WITH RESPECT TO ANOTHER CURVE

The red curve is the symmetric image of the blue one with respect to the green one

On an idea of Robert March.

Derivation of : write , with u and v linked by .
Special case where is the axis Ox: .

The symmetric image of a curve with respect to a curve is the locus of the symmetric images of the points on the curve with respect to the tangent to at a point M located on the normal to at .
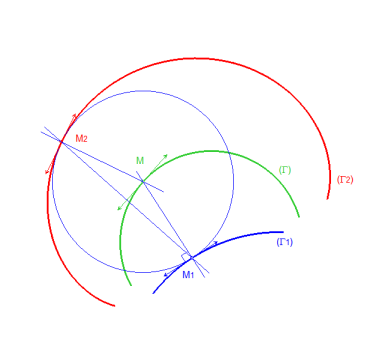Therefore, it also is, in general, the second part of the envelope of the circles centred on and tangent to (each circle having two characteristic points).

It can also be seen as the curve such that the equidistance curve of and is included in .
Only "included" as we can see on the example opposite: the two blue and red semicircles are symmetric images of one another with respect tot the green diameter, but the equidistance "curve" is reduced to the centre.

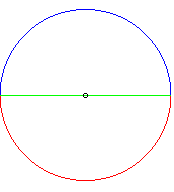Some properties:
If is a line, we get, of course, the classic axial symmetry.
Like this latter symmetry, the symmetry is "in general" involutory: if there is a one-to-one correspondence between and then the symmetric image of is .
Two parallel curves have parallel symmetric images (with the same gap).
The symmetric images of two secant curves intersect with the same angle (but opposite sign)
A curve is its own symmetric image with respect to its evolute.

Examples:

If reduces to a point O, its symmetric image with respect to is none other than the orthotomic of with respect to O.
We derive from this that the symmetric image with respect to of a curve parallel to the orthotomic of with respect to O is a circle centred on O.
For example, the symmetric images of the lines parallel to the directrix of a parabola, with respect to this parabola, are circles centred on the focus (since the orthotomic of a parabola with respect to its focus is the directrix).
The symmetric image of the tangent at the vertex of a parabola, with respect to this parabola, is the circle centred on the focus and tangent at the vertex.

Similarly, the symmetric images of the circles centred on a focus of a centred conic, with respect to this conic, are the circles centred on the other focus (since the orthotomic of the conic with respect to a focus is the directrix circle centred on the other focus).

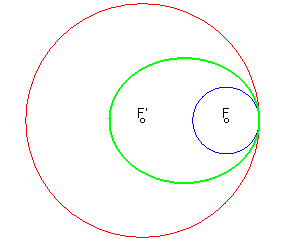The nephroid is the symmetric image of a diameter of a circle with respect to this circle.

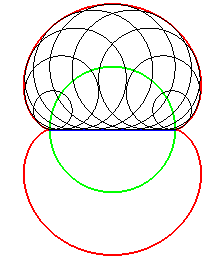More generally, the epicycloid and the hypocycloid that have the same cusps are symmetric images of one another with respect to the base circle.
This comes from the fact that if two curves roll symmetrically on a curve, then the corresponding roulettes are symmetric images of one another with respect to this curve.
Opposite, the astroid, and the epicycloid with 4 cusps are symmetric images of one another with respect to the base circle.

The same holds for the epi- and hypo-trochoids.
Opposite, in the shortened case, and the elongated case.

Symmetric image of the axis of a sinusoid, with respect to that sinusoid.
Parametrization: .

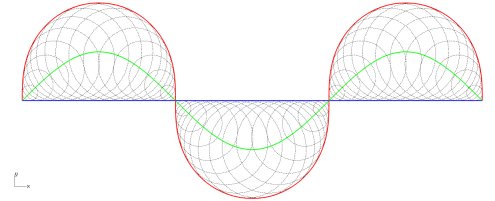Below, a few curiosities: symmetric images of curves with respect to themselves (parabola, ellipse, hyperbola, deltoid).
Only the first one has a simple equation:

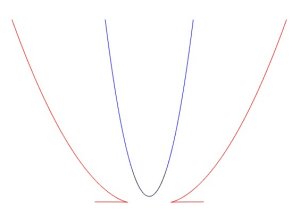
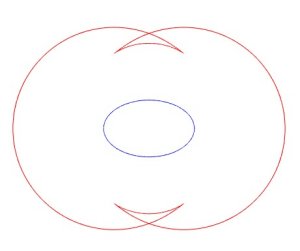
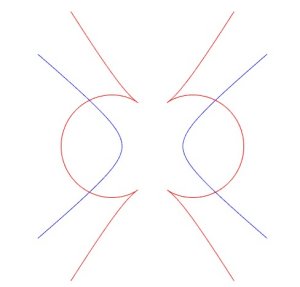
next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

The symmetric image of a curve with respect to a curve is the locus of the symmetric images of the points on the curve with respect to the tangent to at a point M located on the normal to at . Therefore, it also is, in general, the second part of the envelope of the circles centred on and tangent to (each circle having two characteristic points).
It can also be seen as the curve such that the equidistance curve of and is included in . Only "included" as we can see on the example opposite: the two blue and red semicircles are symmetric images of one another with respect tot the green diameter, but the equidistance "curve" is reduced to the centre.