Two curves joining a point A to a point B, placed in a uniform gravitational field are said to be synodal if, when two massive points are dropped from A with no initial speed, both the points arrive simultaneously at B, whether they follow one curve or the other.
 

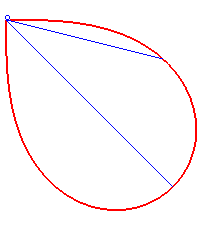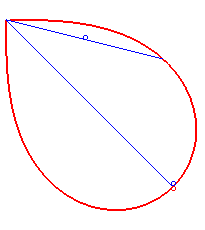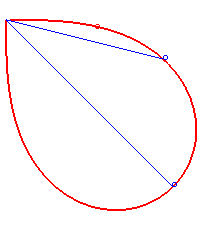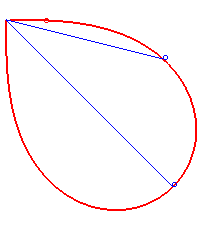
Bonati posed and solved in 1780 the problem of determining a curve starting from O such that, at every instant, the time taken to arrive at the point M along this curve is equal to the time a massive point starting from O would take to arrive at M along the line (OM); in other words, of determining a curve that would be synodal with all its secants passing by one of its points. The answer is a half-lemniscate of Bernoulli.
 

See also at synchronous curve, isochronous curve of Huygens, isochronous curve of Leibniz, isochronous curve of Varignon, brachistochrone and tautochronous curve.
 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2017