TROCHOID


| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
TROCHOID


| Curve studied by Dürer in 1525 and Rømer
in 1674.
From the Greek trokhos: wheel. |
| Cartesian parametrization: |
The notion of trochoid refers to the curve described by a point linked to a disk with radius R rolling without slipping on a line (D); in other words, in it a roulette of a movement of a plane over a fixed plane the base of which is a line and the rolling curve of which is a circle.
For d < R, the curve is also called curtate
cycloid and looks like a sinusoid, and it is one if the term
is neglected in x.
For d = R, we get the cycloid.
For d > R, the curve is also called prolate
cycloid and can assume various shapes, with more and more double points
as d increases.
| The fact that the prolate cycloid has a loop is at the
origin of the following paradox:
Show that, in a train, there always is a portion of mass that moves in the opposite direction of the train. Answer: the bottom of the small edge of the wheels. |
 |
| The trochoids can also be defined as the trajectories
of a movement composed of a uniform linear motion and a circular motion,
with complex parametrization: The ratio 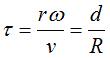 "translation speed over rotation speed" then entirely defines the trochoid,
up to similarity, the elongation increasing with
"translation speed over rotation speed" then entirely defines the trochoid,
up to similarity, the elongation increasing with Opposite, two remarkable cases where the prolate cycloid
is tangent to itself.
|

 |
Concrete examples:
|
- you are walking regularly along a blackboard holding a chalk stick in your hand with a regular circular motion: you are tracing a trochoid, in general, prolate because you are moving slower than your hand is turning. - reflectors on the spokes of the wheels of your bike describe curtate cycloids. - the pedal of your bike describes, when you push down
on it, a trochoid with ratio - the impeller of a boat describes a curtate trochoid
because the grip of the blades in the water is not perfect (the speed of
the end of the blade is greater than the speed of the boat).
|
  |
| The projections of a circular helix on a fixed plane give all the possible shapes of trochoids, potentially scaled; in other words, the trochoids are, up to scaling, the views in parallel perspective, or the shades, of a spring (Montucla-Guillery theorem). |  |
See also the epi-
and hypotrochoid, the
mascot curve , the
Duporcq
curve, and the
minimal
surface of Catalan.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017