Sextique de Cayley

SEXTIQUE DE CAYLEY
Cayley's sextic, cayleysche Sextik

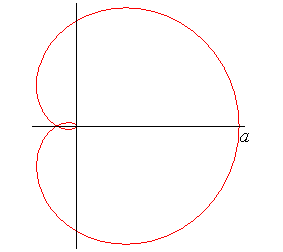
Courbe étudiée par Maclaurin en 1718 et Cayley en 1867.
Arthur Cayley (1821-1895) : mathématicien anglais.

Équation polaire : .
Paramétrisation cartésienne rationnelle : (t = tan q ).
Équation cartésienne : .
Sextique. tricirculaire. rationnelle.
Abscisse curviligne : .
Angle tangentiel polaire : .
Rayon de courbure : .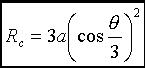
Équation podaire : .
Longueur : .

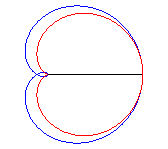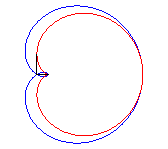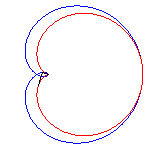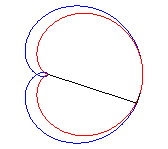
La sextique de Cayley est la podaire de la cardioïde par rapport à son point de rebroussement (ici, la cardioïde est ).

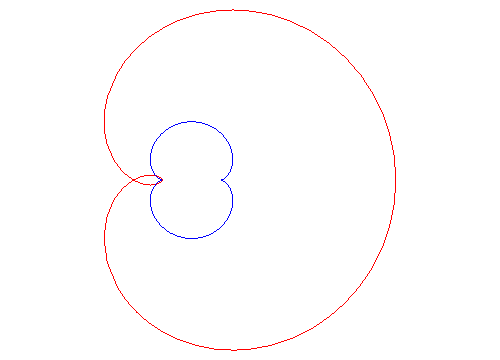
C'est aussi l'inverse de la cubique de Tschirnhausen par rapport à son foyer.

C'est un cas particulier de spirale sinusoïdale et on la retrouve aussi comme lieu du sommet d'une parabole tangente à un cercle fixe et de foyer un point de ce cercle (ici, le cercle de centre O et de rayon 2a, voir Aubert et Papelier tome 2 p. 320)

Sa développée est la néphroïde centrée en (a/2, 0) et passant par O.

La néphroïde ayant aussi pour développée une néphroïde, la sextique de Cayley est l'une des courbes parallèles à la néphroïde.