CUBIQUE CIRCULAIRE RATIONNELLE DROITE
Right
circular rational cubic, gerade rationale KreisKubik
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
CUBIQUE CIRCULAIRE RATIONNELLE DROITE
Right
circular rational cubic, gerade rationale KreisKubik

| Autres nom :
- cissoïde droite allongée ou hypercissoïde droite (cas crunodal), cissoïde droite raccourcie ou hypocissoïde droite (cas acnodal). - courbe de Cramer. |
| Équation polaire : Paramétrisation cartésienne : Équation cartésienne : Cas
|
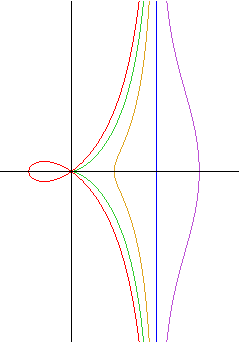 |
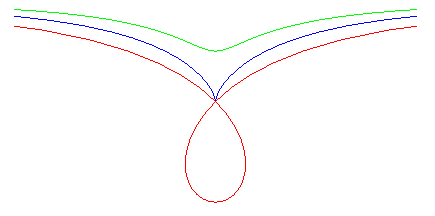
Les cubiques circulaires rationnelles sont dites droites lorqu'elles ont un axe de symétrie ; elle sont dites crunodales, cuspidales ou acnodales suivant que le point singulier est un point double à tangentes distinctes, un point de rebroussement ou un point isolé.
Elles possèdent la propriété d’avoir
6 constructions géométriques remarquables équivalentes.
| 1) Construction cissoïdale.
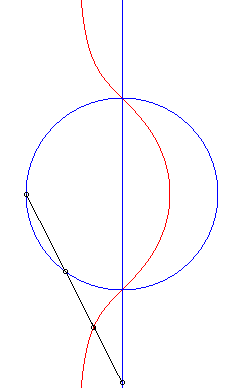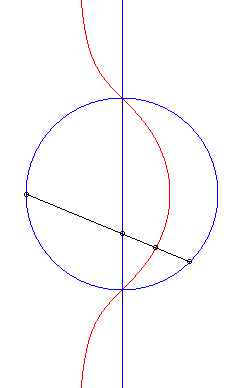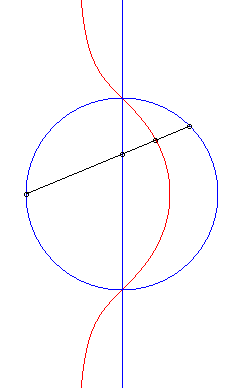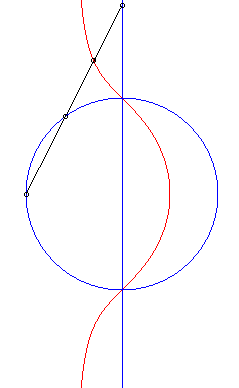
Ces courbes sont les cissoïdales de cercle et droite par rapport à un point O du cercle, la droite étant perpendiculaire au diamètre du cercle passant par O (ici, cissoïdale du cercle (C) passant par O de centre A(b/2, 0) et de la droite (D) : x = a relativement à O). Ces cubiques, qui ont (D) pour asymptote et O pour point singulier, sont crunodales, cuspidales, ou acnodales suivant que la droite (D'), symétrique de (D) par rapport à O, est sécante, tangente, ou extérieure au cercle (C). Ci-contre, construction équivalente comme médiane polaire de cercle et droite, issue de l'écriture |
 |
| 2) Construction comme cubique
de Sluze.
Un point P parcourant la droite (D), la cubique est le lieu de M de la droite (OP) défini par |
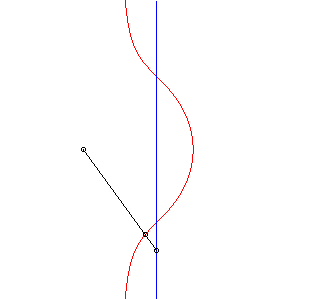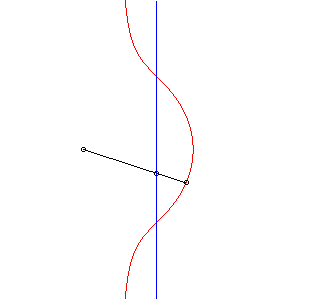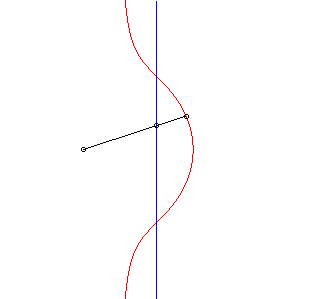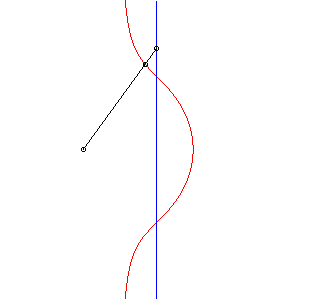 |
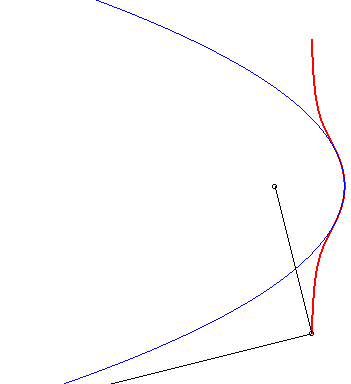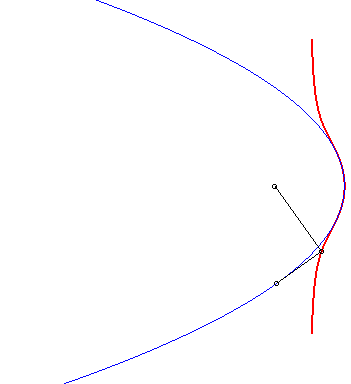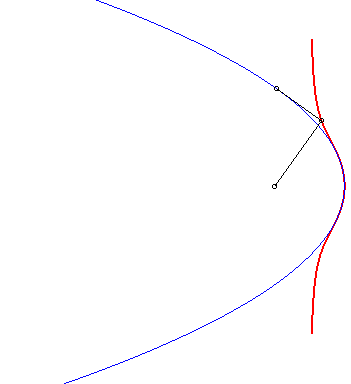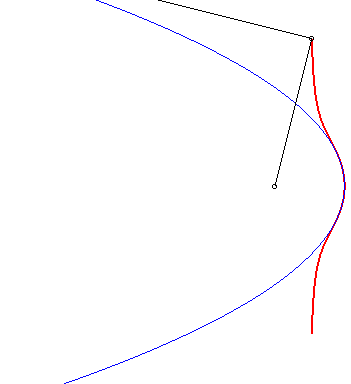
| 3) Construction par podaire.
Ces cubiques sont les podaires de paraboles par rapport à un point de l'axe de la parabole. On obtient le cas crunodal, cuspidal, ou acnodal suivant que le point O est extérieur à la parabole, sur la parabole ou intérieur à la parabole. |
 |
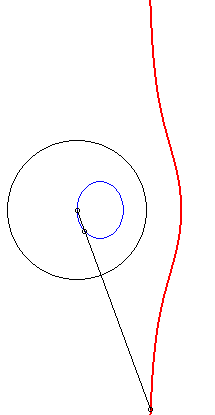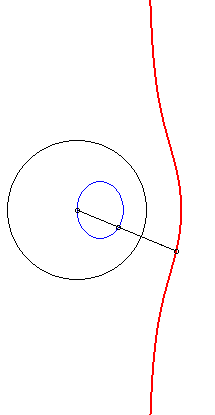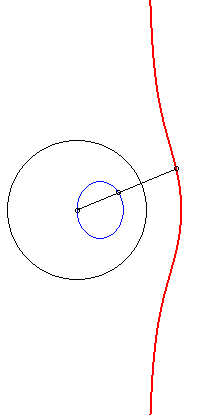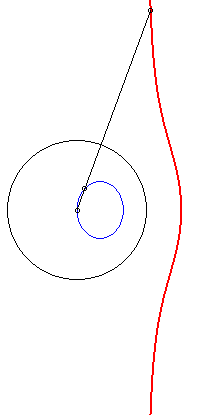
| 4) Construction par inversion.
Ces cubiques sont les inverses de coniques par rapport à un de leurs sommets. La cubique est crunodale, cuspidale, ou acnodale suivant que cette conique est une hyperbole, une parabole ou une ellipse. |
 |
| 5) Construction comme kiéroïde. |
 |
| 6) Construction comme glissette
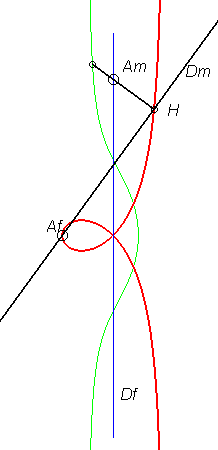
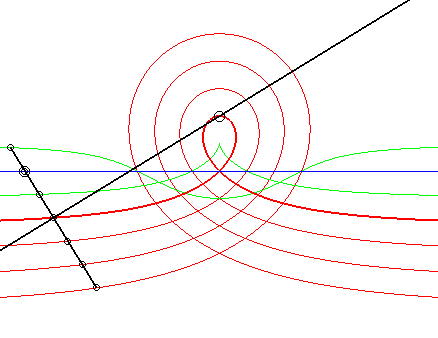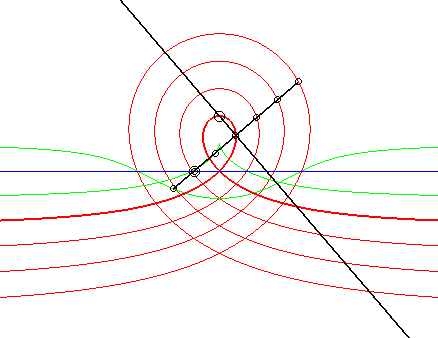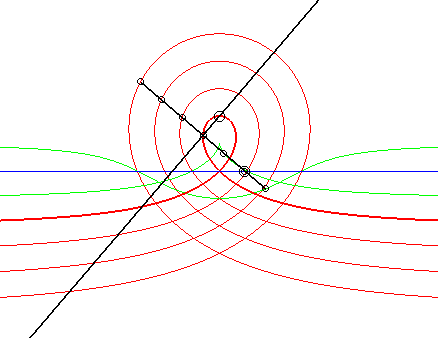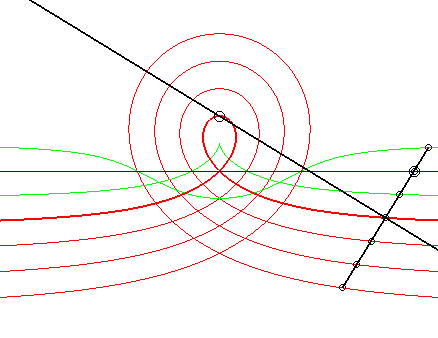
obtenue par la méthode de l'équerre de Newton.
Un mouvement plan sur plan est défini par le fait
qu'une droite Dm
du plan mobile passe par un point fixe Af
et qu'un point Am
du plan mobile décrit une droite fixe Df,
la distance entre le point et la droite fixe étant égale
à la distance entre le point et la droite mobiles.
Plus précisément, le barycentre M de H affecté du coefficient u et de Am affecté de 1– u décrit la cubique circulaire rationnelle droite avec b = –a u. Lorsque M est au milieu I de [H Am], on obtient la cissoïde, lorsqu'il est du côté de Ampar raport à I, on obtient les cubiques acnodales, et de l'autre côté, les cubiques crunodales. |
 |
 |
 |
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL
2011