Courbe isoptique

COURBE ISOPTIQUE
Isoptic curve, isoptische Kurve

L'isoptique d'angle de la cardioïde est formée de deux limaçons de Pascal.

Courbe étudiée par La Hire en 1704 et Chasles en 1837.
Du grec Isos "égal" et optikos "relatif à la vue".
Appellation donnée par Taylor en 1884 [Note on a theory of orthoptic and isoptic loci, Proc. R. S., London, T. XXXVII,1884].

Une méthode pour obtenir l'équation de l'isoptique de la courbe f(x,y)=0 : éliminer x1,y1,x2,y2 entre les 5 équations : f(x1,y1)=0, f(x2,y2)=0, p(x1,y1)*(x-x1)+q(x1,y1)*(y-y1)=0, p(x2,y2)*(x-x2)+q(x2,y2)*(y-y2)=0, et tan(alpha)=(p(x1,y1)-p(x2,y2))/(1+p(x1,y1)*q(x2,y2)).

En géométrie différentielle, la (courbe) isoptique d'angle d'une courbe est le lieu des points d'où l'on peut mener deux tangentes à la courbe formant un angle .

Exemples :

- les isoptiques de la parabole sont des hyperboles (de même foyer et directrice que la parabole), d'équation : .
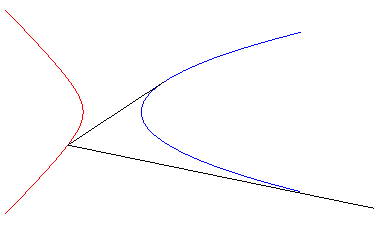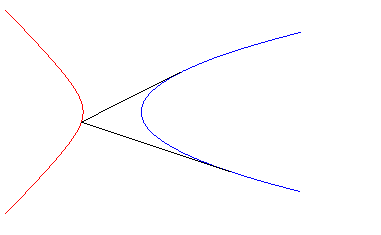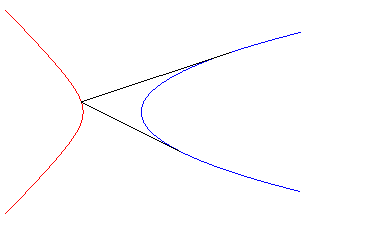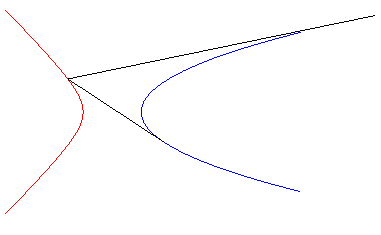Ci-contre le cas d'un angle (l'autre branche de l'hyperbole donnerait l'angle supplémentaire).

    - les isoptiques des coniques à centre sont les spiriques de Persée : pour la conique , l'isoptique a pour équation (Loria 2D tome 2 p. 156).
    - les isoptiques des (- épi, - hypo) trochoïdes sont des réunions de (- épi, - hypo) trochoïdes (voir l'exemple de la cardioïde ci-dessus).
    - les isoptiques des spirales sinusoïdales sont des spirales sinusoïdales.

Une notion voisine en géométrie métrique, portant le même nom, est celle d'isoptique d’angle d'une partie X du plan : lieu des sommets des secteurs angulaires d'angle circonscrivant X (c'est-à-dire contenant X, et dont les deux côtés rencontrent X).

Exemples :
- les isoptiques d’un segment de droite sont les cercles ayant ce segment pour corde (théorème de l’arc capable).

A été également désigné par isoptique une notion différente : l'isoptique de deux parties X et Y du plan est le lieu des points du plan d'où l'on "voit" X et Y sous le même angle, plus précisément, le lieu des sommets de deux secteurs angulaires de même angle, l'un circonscrivant X, l'autre Y.

Lorsque les deux parties X et Y sont des segments de droite, on obtient les cubiques isoptiques.

Le cas de deux cercles de centres , et de rayons est beaucoup plus simple : on obtient les cercles d'Apollonius d'équation .

courbe suivante courbe précédente courbes 2D courbes 3D surfaces fractals polyèdres