COURBE SYMÉTRIQUE D'UNE COURBE PAR RAPPORT À
UNE AUTRE
Symmetric
image of a curve with respect to an other one, symmetrische Kurve einer
Kurve zu einer anderen

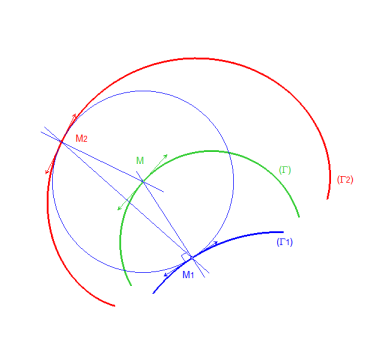
La rouge est la symétrique de la bleue par rapport à
la verte
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
COURBE SYMÉTRIQUE D'UNE COURBE PAR RAPPORT À
UNE AUTRE
Symmetric
image of a curve with respect to an other one, symmetrische Kurve einer
Kurve zu einer anderen

La rouge est la symétrique de la bleue par rapport à
la verte
| Sur une idée de Robert March. |
| Obtention de Cas particulier où |
| La courbe symétrique d'une courbe C'est donc aussi, en général, la deuxième partie de l'enveloppe des cercles centrés sur |
 |
|
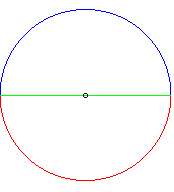
On peut aussi la voir comme la courbe Seulement "incluse" comme on peut le voir sur l'exemple ci-contre : les deux demi-cercles bleus et rouge sont symétriques par rapport au diamètre vert, mais la "courbe" d'équidistance est réduite au centre. |
 |
Quelques propriétés :
Si
est une droite, on obtient bien sûr la symétrie axiale classique.
Comme pour cette dernière, cette symétrie
est "en général" involutive : si la correspondance entre
et
est
bijective, la symétrique de
est
.
Deux courbes parallèles,
ont des symétriques parallèles (avec le même écart).
Deux courbes sécantes ont des symétriques
se coupant sous le même angle qu'elles (avec inversion du signe).
La courbe symétrique d'une courbe par rapport
à sa développée est elle-même.
Exemples :
| Si On en déduit que la symétrique par rapport à Par exemple les symétriques des droites parallèles à la directrice d'une parabole, par rapport à cette parabole, sont des cercles centrés au foyer (l'orthotomique d'une parabole par rapport à son foyer étant la directrice). |

La courbe symétrique de la tangente au sommet d'une parabole, par rapport à cette parabole, est le cercle centré au foyer et tangent au sommet. |
||
| De même, les symétriques des cercles centrés en un foyer d'une conique à centre, par rapport à cette conique, sont des cercles centrés à l'autre foyer (l'orthotomique de cette conique par rapport à un foyer étant le cercle directeur centré en l'autre foyer). |
 |
||
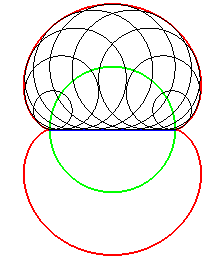
| La néphroïde est la symétrique d'un diamètre d'un cercle par rapport à ce cercle. |
 |
||
| Plus généralement, l'épicycloïde
et l'hypocycloïde ayant
les mêmes rebroussements sont symétriques par rapport au cercle
de base.
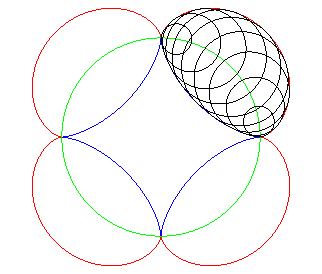
Ceci vient du fait que si deux courbes roulent symétriquement sur une courbe, les roulettes correspondantes sont symétriques par rapport à cette courbe. Ci-contre, l'astroïde,
et l'épicycloïde à 4 rebroussements sont symétriques
par rapport au cercle de base.
|
 |
||
| Même chose pour les épi- et hypo-trochoïdes.
Ci-contre, le cas raccourci, et le cas alllongé. |
|
||
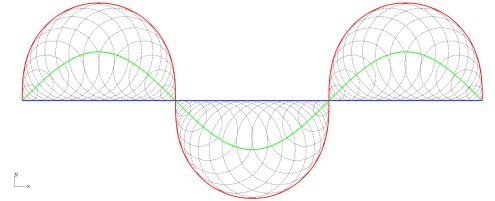
| Symétrique de l'axe d'une sinusoïde, par
rapport à cette sinusoïde.
Paramétrisation : |
 |
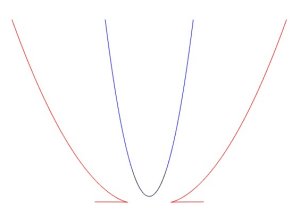
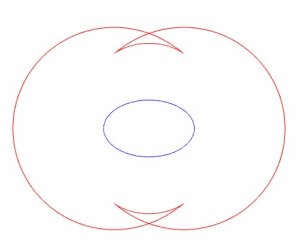
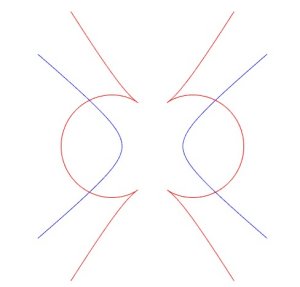
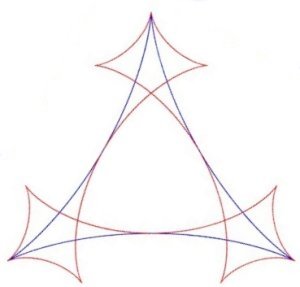
Ci-dessous, quelques curiosités : des symétiques
de courbes, par rapport à elles-mêmes (parabole, ellipse,
hyperbole, deltoïde).
Seule la première a une équation simple
:
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2016