RECTANGULAR BILLIARD KNOT AND LINK

The " (6,2) "
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
RECTANGULAR BILLIARD KNOT AND LINK

The " (6,2) "
| Studied by Jones
and Przytycki in 1998.
Links: undergraduate research work on billiard trajectories Constructing the (5,3) by hand! Images made by Alain Esculier. |
A rectangular billiard knot is the knot
obtained from the closed trajectory of a ball on a billiard with rectangular
edge, by modifying the crossing points in alternate above/below passages.
| If the dimensions of the billiard are L,L' and
the ball starts rolling from a side with length L (and not in the
corner) following a trajectory forming a slope a with respect to
this side, then the trajectory is closed iff the ratio L/L' over
a
is a rational number p/q (with p and q coprime).
In this case, the ball bounces p times on the sides with length L and q times on the sides with length L'. All in all, there are |
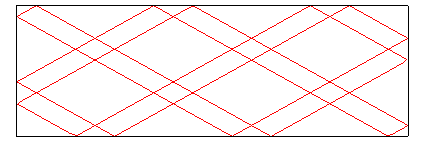
Here p = 5 and q =3; 5 bounces for each horizontal side,
3 for each vertical side,
|
| Except the cases for which they start at a corner, the curves have the same topology, and therefore yield a unique knot, that we call of type (p, q). |
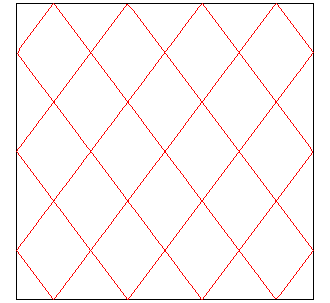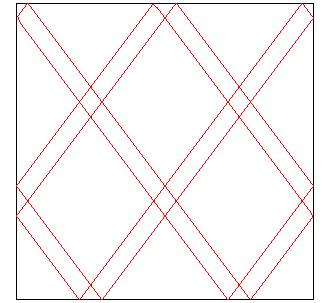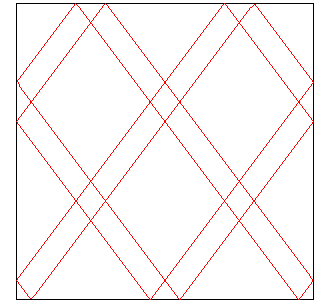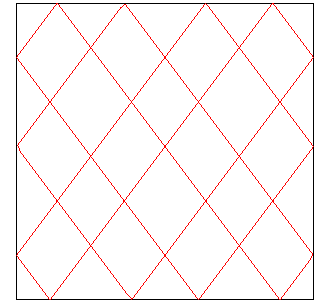 |
| Up to a scaling, we can suppose
- that the billiard is a square (and the slope is equal to p/q), - or that L/L'=p/q, in which case the slope is equal to one (the crossings form right angles). |
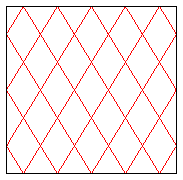 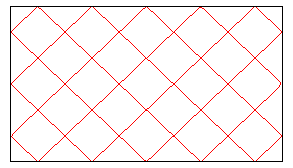 |
| The billiard knot of type (p,q) can also be obtained
from the planar
Lissajous curve.
Indeed, if c is an even, continuous function decreasing on For For |
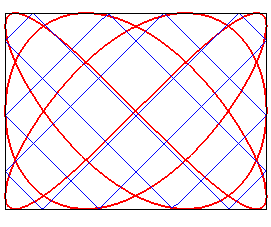
case p = 4, q = 3 |
| The above/below alternation can be obtained by a 3D Lissajous
curve, or, which is equivalent, by the trajectory of a ball (not subject
to gravitation) in a parallelepipedic billiard.
Equation with the above notations: See at Lissajous knot. |
 |
Examples:
| q = 1: the knot is trivial | p = 3, q = 2: we get the fourth prime knot with 7 crossings. | p = 4, q = 3, prime knot with 17 crossings. | p = 5, q = 3 |
 |
 |
 |
 |
| Artistic productions: Buddhist, Islamic, Celtic, Roman, or maritime art! |
 Picture taken in Kathmandu: B. Ferreol. |
Image taken from the very interesting blog Nico-matelotage. |

Celtic knot |
Variations and generalizations:
1) For p and q non coprime, if we trace all the trajectories with p evenly spaced bounces on two opposite sides, and q bounces on the two other sides, then we get a link with gcd(p,q) components.
Examples:
| p = 2, q = 2: we get Solomon's knot, the simplest non trivial link | p = 3, q = 3: link with 12 crossings and 3 components, indexed by 12x-3-79 in knotilus. Sometimes called triple Solomon knot. | p = 4, q = 2: link with 10 crossings and 2 components, indexed by 101 in knot-atlas. | p = 4, q = 4.
Quadruple Solomon knot. |
p = 8, q = 8 |
 |
 |
 |
 |
 |
|
Roman mosaic |

Islamic link (Marrakech) |

Mongolian pattern, that can be found as a decoration in yurts |

Roman mosaic (villa casale) |
 |
| The graph of the Turk's head of type (p,q) (coprime or not) is a rectangular grid of p–1 times q–1 squares; opposite, the case (5,3). | 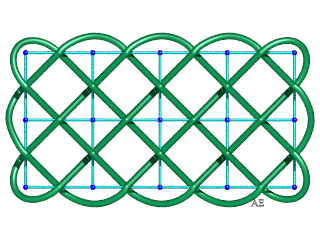 |
2) We can also consider the curves obtained when the ball starts from a corner. In this case, the curve is open, but can be closed in various ways; and we can superimpose several curves.
Examples in the case (3,2):
Closing only one open curve creates a trivial knot, but
the superimposition of two open curves is interesting.
It is the Carrick
bend which leads, after closing, either to the 18th
prime knot with 8 crossings : 8.1.18, or to the 7th
prime link with 8 crossings and two loops: 8.2.7.
 |
 |
 |
 |

Knot 8.1.18 |

|
Examples in the case (4,3):
| If the curve is closed, we get the trefoil knot. | If two open curves are superimposed and the different blades connected, we get a knot with 18 crossings indexed by 18x-1-230179 in knotilus; it is used in the fabrication of doomarts. | If the identical blades are connected, we get a link with 18 crossings indexed by 18x-2 - 410219 in knotilus. |
 |
 |
 |
 |
 |
|
Example in the case (7,3):
| Example in the case (1,1); closing gives the Whitehead link. | Example in the case (3,3): |
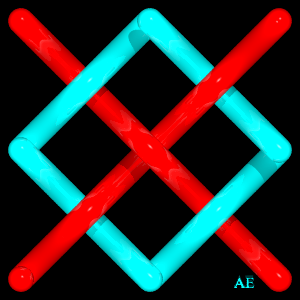 |
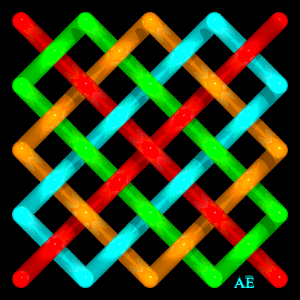 |
3) We can also consider non alternate above/below crossings.
We get knots for which the minimal crossing number is
less than the number of crossings of the curve.
 |
 |
 |
| Above, two crossings can be unfolded (top-right): we get the knot 5.1.2. | Here, 4 crossings can be unfolded, we get the trefoil knot. | This knot was obtained by following the billiard ball with a passage below when we cross a previous line. Therefore, we can unfold starting from the end. Since this works every time, there always exists a configuration yielding the trivial knot. |
4) The rectangular billiard can be replaced by a convex
polygonal billiard.
With any type of crossings, we can get all the possible
knots, even by only considering billiards the edge of which is a regular
polygon. Indeed, every knot
has a projection that is a crossed regular polygon. See also the polygram
knots.
| With a triangular billiard, for example, we get the trefoil knot: |
 |
|
| 4 loops link got with a cruciform billiard.
On the right, variant with an additional loop, idea of Alain Esculier. |
 |
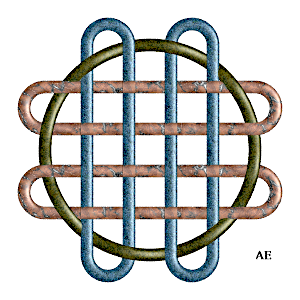 |
| This roman mosaik from the Gallo-Roman villa of Seviac represents an interlacing which is found to be obtained by the routes of two balls in a cruciform billiard. |
 |
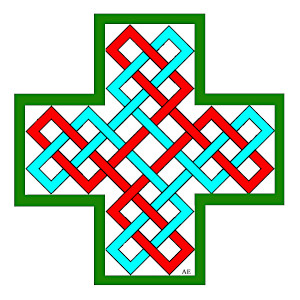 |
See also the cylindrical billiard knots, or Turk's heads, the linear Celtic knots.

Frontispiece of the chapel of Murato in Corsica: it is a (22,3).
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2018