The curves (G1) and (G2) are parallel if we can determine current points M1 and M2, respectively, such that and . For an initial curve with current point , a parallel is a set (Ga) of points where , the angle being the torsion angle (see the notations). The surface area of the strip between two corresponding arcs of (G0) and (Ga) is equal to the length of the medial arch of (Ga/2) times a, this under the condition that the strip does not overlap itself and that a is always less than the radius of curvature.

Two curves are said to be parallel if every plane normal to one is normal to the other; and it can be proved that, in this case, the distance between two points on the same normal plane is constant; do not mistake with curves that are the translation of one another.

Therefore, two curves are parallel if they are the ends of a segment line of constant length that always moves perpendicularly to its direction, which is equivalent to the fact that the line supporting this segment has an envelope and rolls without slipping on it; this curve is then the common evolute of the two parallels. And the parallels are the involutes of this curve.

In more concrete terms, two parallel curves can therefore be seen as two rails of a railroad connected by crossties of constant length, the crossties always being perpendicular to the rails.

The parallelism relation of 3D curves is an equivalence relation; an equivalence class is the set of trajectories of points connected to a plane that rolls without slipping on a developable surface, which is the common polar developable of all these curves (hence a one-to-one correspondence between the developable surfaces and the equivalence classes of parallel curves).
The curves parallel to a curve are therefore the involutes of its polar developable.

The surface generated by the lines joining two corresponding points on the two parallels is a developable surface (and every developable surface can be generated this way): two curves are therefore parallel if and only if they are two orthogonal trajectories of the generatrices of a developable surface.

For the expression of the parallel curve, we have to consider and not where is the normal vector (the vector is defined so that the torsion cancels):
 

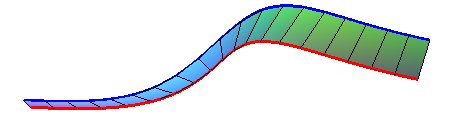
A horopter curve (in blue) and a curve of the type The "crossties" are indeed perpendicular to the blue curve, but not to the red one.

The same horopter curve and a parallel curve, of the type

A curve can be parallel to itself; in addition to the examples in the planar case, there is, in 3D, the edge of a Möbius strip, in the case where its representation is developable and the edge is perpendicular to the generatrices of the surface.
 

A Möbius strip with 3 half-turns) with self-parallel edge (composed of strips of 3 cones centered on the vertices of the big triangle).

The surfaces that are the reunion of curves pairwise parallel are the Monge surfaces.
 
 

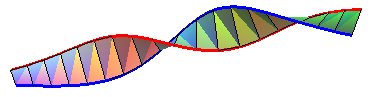
The two rails of this roller-coaster are parallel:

 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

Acknowledgment: thanks to Samuel Boureau for his article "serpentins et tubes" in an APMEP report, only place where I found a definition of parallels in space.

© Robert FERRÉOL 2018