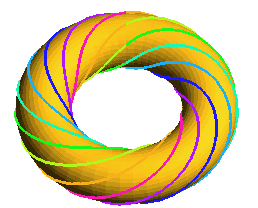
one color = one turn around the axis
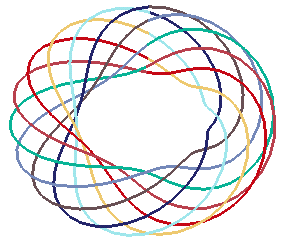
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
TORIC SOLENOID, KNOT AND LINK
|
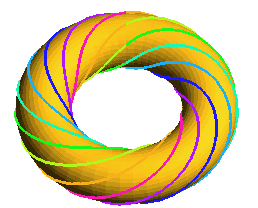
one color = one turn around the axis |
|
| Websites:
Wikipedia Knot atlas |
Cylindrical equation: 
(n > 0)
Cartesian parametrization:  .
Curvilinear abscissa:  . |
The toric solenoids are the solenoids
the central curve of which is a circle; therefore, they coil evenly around
a torus. They can also
be seen as the trajectory of a point with a uniform circular motion in
a plane turning uniformly around an axis.
The toric solenoids are also obtained as the intersection
between the generalized
Plücker's conoid: 
and the torus with center O and major and minor radii R and
r. Opposite, the cases n = 2 and 3: the intersection is composed
of several rotated solenoids. |
 |
 |
When the torus is reduced to a sphere (R = 0),
we get the clelias.
The projections on xOy are the conchoids
of roses.
spindle torus |
 |
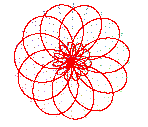
View from above: conchoid of a rose |
 |
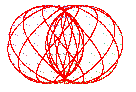open torus |
 |
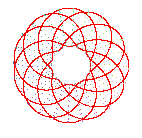
View from above: conchoid of a rose |
 |
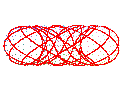When n is a rational number p/q, and R > r, the curve is closed and simple, and the knot associated to the corresponding toric solenoid is the torus knot T(p, q), that has p coils around the torus and q turns around the axis, and always is a prime knot. The knots T(p, q) and T(q, p) are equivalent (to go from (p,q) to (q,p), pass a needle in the bore of the torus).
Every knot that has a representation without crossings
on the torus is a torus knot of this type.
Every right section of the tube has q blades and
the view from above shows p (q – 1) crossings; it was proved
that for p > q, this number of crossings is the minimal number
of crossings of the corresponding knot, (the latter is therefore equal
to q (p – 1) for p < q).
| For n = 1 (and also for any n integer or reciprocal of an integer), we get the trivial knot (but contrary to what might be expected, the solenoid is not a Villarceau circle of the torus). |  |
For q = 2 (respectively p = 2), we get knots
with p (respectively q) crossings:
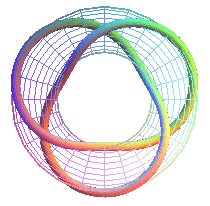
T(3,2): trefoil knot prime knot 31 |
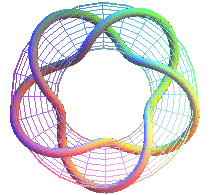
T(5,2): pentagram prime knot 51 |
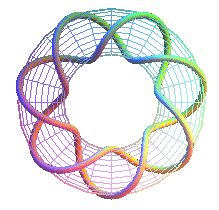
T(7,2): first heptagram prime knot 71 |
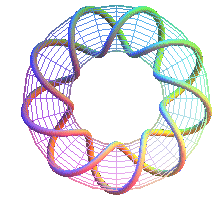
T(9,2): first nonagram prime knot 91 |
 |
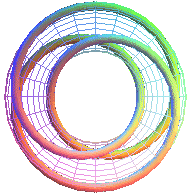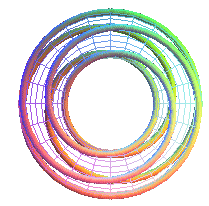
T(2,5) |
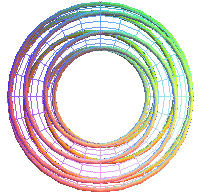
T(2,7) |
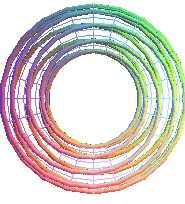
T(2,9) |
T(4,3) equivalent to the 19th prime knot with 8 crossings |
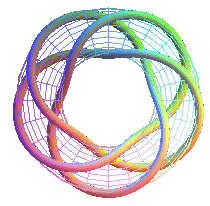
T(5,3) equivalent to the 124th prime knot with 10 crossings |
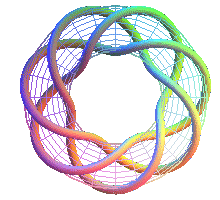
T(7,3) second heptagram |
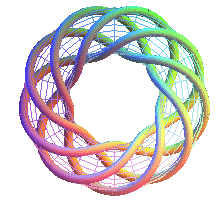
T(9,4) third nonagram |
The toric solenoids for q = 2 are edges of Möbius
strips with p torsions:
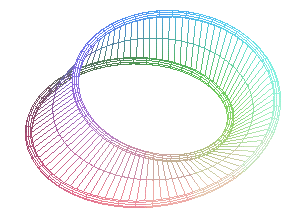
n = 1/2: edge of the classic Möbius strip (one torsion) |
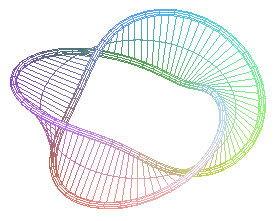
n = 3/2: edge of the Möbius strip with 3 torsions |
When p and q are not coprime, if we write
d = gcd(p, q), p' = p/d, q' = q/d, n = p/q = p'/q',
the toric solenoid of type (p', q') and its d – 1 images
by consecutive rotations of angle 
around the axis of the torus form a link
of d torus knots of type (p', q'), called torus link T(p,
q). It is also a prime link with minimal number of crossings p
(q – 1) for p > q
(?). |
 |
Here are some examples:
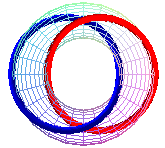
T (2,2), Hopf link, prime link 212 |
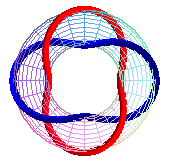
T(4,2), Solomon's knot, prime link 412 |
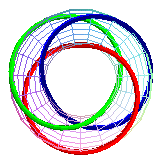
T(3,3), prime link
633
|
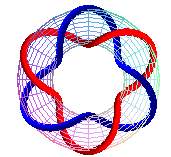
T(6,2), prime link 612 |
T(6,3) |
T(6,4), two interlaced trefoil knots |
T(8,2) prime link 812 |
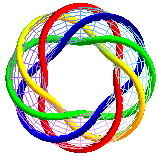
T(8,4) |
T(8,6) |
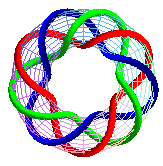
T(9,3) |
We can make the torus link T(p,
q)
by placing q blades of the same length side by side and applying
a torsion of p/q turns and glueing the blades at their ends.
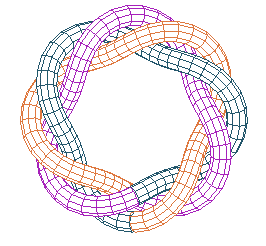
For example, for the knot (8, 3), there are three glued blades after a torsion of 8/3 turns |
The same knot in a sculpture by J. Robinson Philip Trust Collection |
The torus knots are also sometimes defined on the Clifford
torus; their parametrization is much simpler: 
;
by identification of 
and 
, they
can also be seen as the image of the unit circle 
by the map: 
.
The torus knots and links for p > 2q are
equivalent to the polygram knots
and links.
They are also the "edges" of the rotoidal
prisms.
The torus knot T(n, n–1) is equivalent
to the n-leaved trefoil
knot.
Compare to the Turk's
heads, that have the same view from above, but with alternate crossings.
Also compare to the geodesics
of the torus.
 |
Mexican company |
|
Engraving by Escher |
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2018