LINE OF EXTREME SLANT
| Notion studied by Barre de Saint
Venant in 1852 and Boussinesq in 1871. |
Given a vertical direction, the lines of extreme slant of a surface are the topographic lines, traced on the surface, composed of the points where the slope (of the section of the surface by a vertical plane tangent to the slope line) presents an extremum along the corresponding
contour line.
It can be proved that they are also the lines composed of the points of the slope lines where the osculating plane is vertical, or, and this is equivalent, of the points corresponding to the points with zero curvature of the horizontal projections of the slope lines; in particular, the slope lines that have a linear horizontal projection are lines of extreme slant, and they are the only ones among the slope lines; in this case, they are thalweg or crest lines and it can be proved that they are also precisely the slope lines that are curvature lines.
For the surface 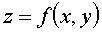 , using the Monge notations: , using the Monge notations: 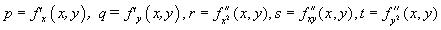
(for a surface parametrized by 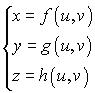 , take , take 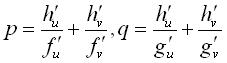 ), the slope being equal to ), the slope being equal to  , ,
its extrema on a contour line are obtained through the implicit equation:
 , i.e. , i.e.  (de Saint Venant relation).
(de Saint Venant relation).
The curvature of the horizontal projections of the slope lines is equal to  . Therefore, it being equal to zero gives the same relation. . Therefore, it being equal to zero gives the same relation.
The additional condition to get a minimum (respectively, a maximum) can be written p²(2s²+t²-tr)-2pqs(r+t)+q²(2s²+r²-tr)+p^3c+p²q(d-2b)+pq²(a-2c)+q^3b>=0
(respectively <= 0) where a,b,c,d are the third derivatives of f. |
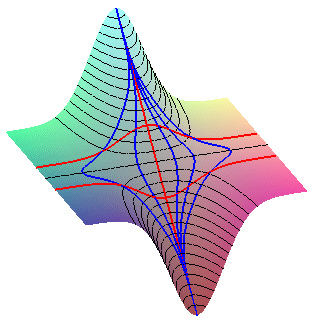
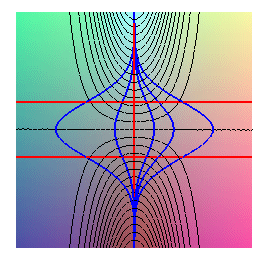
Example #1: the surface z = y exp(-x²):
the contour lines (in black) are given by y = k exp(x²),
the slope lines (in blue) by x = k exp(-y²),
and the lines of extreme slant (in red) by x = 0 and y = +-1/Ö2.
The line of extreme slant x= 0 is linear: it is a slope line, and also a crest for y > 0, a thalweg for y < 0.
Notice that the lines of extreme slant y = +-1/Ö2 do pass, in horizontal projection, through the inflection points of the slope lines. |
 |
 |
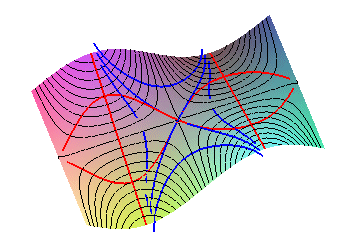
Example #2: the surface z = y sin x:
the contour lines (in black) are given by y sinx = k,
the slope lines (in blue) by exp(y²) cos²
x = k,
and the lines of extreme slant (in red) by x = pi/2 + k pi and y = +-sin x.
The lines x = pi/2 + k pi are linear: they are slope lines, and also crests or thalwegs.
Notice that the lines y = +-sin x do pass, in horizontal projection, through the inflection points of the slope lines. |
 |
General examples:
- the lines of extreme slant of a cone are the directrices that intersect perpendicularly with the contour lines (for a cone 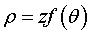 , this corresponds to the extrema of f).
, this corresponds to the extrema of f).
- the lines of extreme slant of a surface of revolution with vertical axis are the meridians.
- the lines of extreme slant of a surface of equal slope with horizontal reference plane are the slope lines.
© Robert FERRÉOL
2018


