FLOW LINE OF A SURFACE

| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
FLOW LINE OF A SURFACE




| Curves studied by C. Piquet in 2002. |
| Differential equation (derived from Newton's second law): This differential system can be written, for a surface with equation z = f(x, y): |
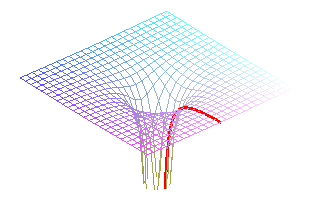
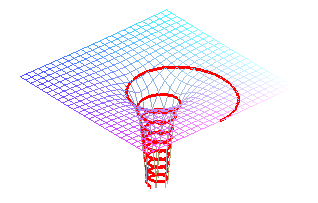
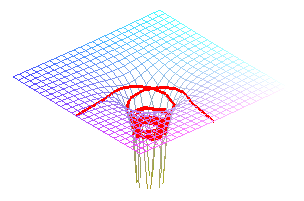
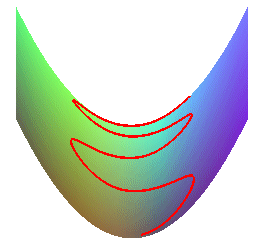
The flow lines of a surface are the trajectories of massive points linked to the surface and subject to a vertical gravitational field (physically, they can be obtained by making a smooth ball roll on the surface).
When the velocity is equal to zero, the flow line is tangent to the slope line passing by the point, but, otherwise, it is not the case in general.
Note that the gravitational acceleration g > 0, does not impact the shape of the curves (even if it does impact the speed at which they are travelled along). On the contrary, if we take g = 0 in the above equations, we find different curves, that are none other than the geodesics of the surface.
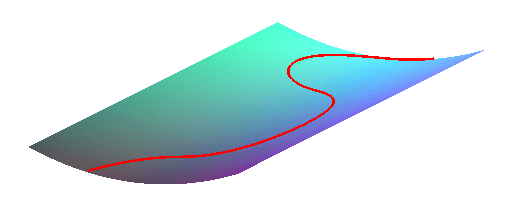
| the flow lines of a tilted plane are parabolas or straight lines. |
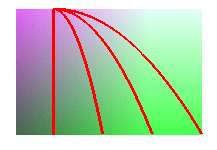 |
| the flow lines of a vertical circular cylinder are the curves that develop onto parabolas or straight lines. |
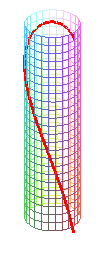 |
| the flow lines of a sphere are none other than the curves of the spherical pendulum. | 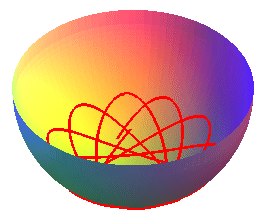  |
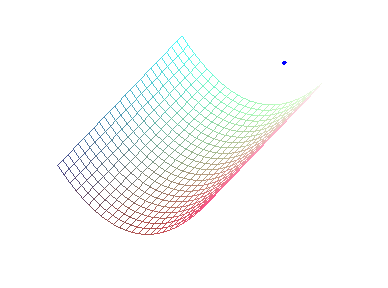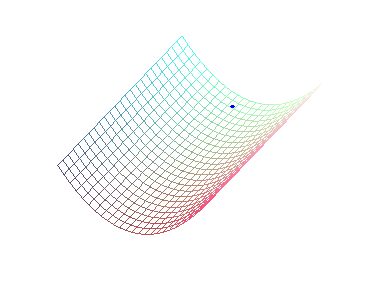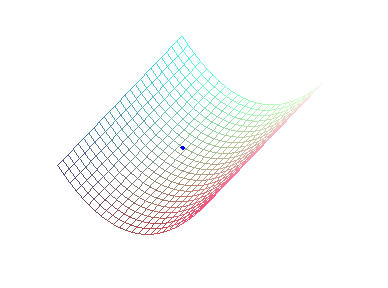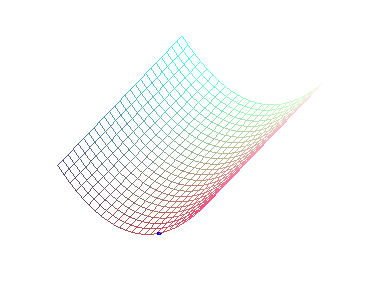
A rain drop falls into the gutter.... |
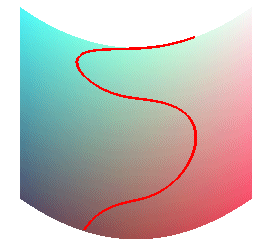 
|
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL, Jacques MANDONNET 2018