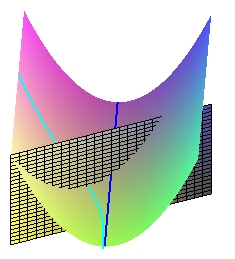
Geographers define the thalweg as the "line joining the bottommost points of the consecutive transverse sections of a valley"; but what is a transverse section? The figure opposite shows that the bottommost point of the section by a vertical plane of an inclined gutter is not necessarily at the center of the gutter, intuitive locus of the thalweg (in deep blue); even worse, the slope line (in light blue) passing by the bottommost point is perpendicular to the plane. The orthogonality does not enable us to recognize the thalweg... The transverse section must be perpendicular to the thalweg... Therefore, to define the transverse section, we must already know the thalweg! The geographic definition can therefore not be taken as the mathematical definition.

Here is a series of definitions that were suggested. We will see that they all have limitations. When the lines defined below go through convex regions, they are crest lines, and when they go through concave regions, they are thalwegs (the points on the surface are said to be "convex" when the section of the surface by a vertical plane tangent to the contour line has a maximum of altitude, "concave" when they have a minimum of altitude). By horizontal reflection, crests and thalwegs are exchanged.
 
 

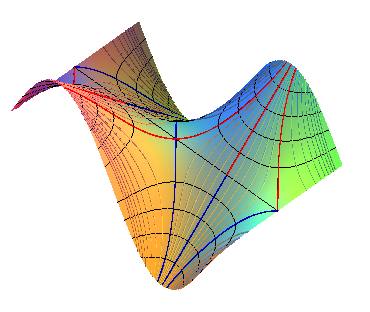
First definition (proposed by Jordan in 1872, used by Dieudonné in Calcul infintésimal for example and used by topographers of the National Institute of Geographic and Forest Information (previously IGN)): the crest and thalweg lines of a surface are the slope lines leading to a saddle; the crest lines refer to the part going up from the saddle, the thalweg lines to the part going down. This definition cannot be defended for at least three reasons: 1: for an unbounded surface like the gutter above, there can be a valley but no saddle! 2: we can always modify the surface locally so that a given slope line would lead to a saddle (or the opposite) and therefore could become a crest line or a thalweg, or not; see also the text by Boussinesq below. 3: a slope line starting from a saddle can very well become asymptotic to another one (see the example opposite): we get a valley with several distinct thalwegs!

Second definition (proposed by de Saint Venant in 1852, and used for example in the Mathematical dictionary by F. Le Lionnais and the one by A. Warusfel).
Given a vertical direction, the crest and thalweg lines are the lines traced on the surface that join the points where the slope (of the section of the surface by a vertical plane tangent to the slope line) has a minimum along the corresponding contour line. In other words, they are the lines of minimum slant.
This definition would formalize the fact that the thalweg is less tilted than the neighboring slope lines that meet it (and the crest line is less tilted that the neighboring slope lines that divert from it).

But this would mean that they would have to be slope lines, which is not the case in general since, in fact, these lines connect the inflection points of the slope lines (in horizontal projection)!

This definition does not allow to detect the crest and thalweg lines the horizontal projection of which is linear.
 

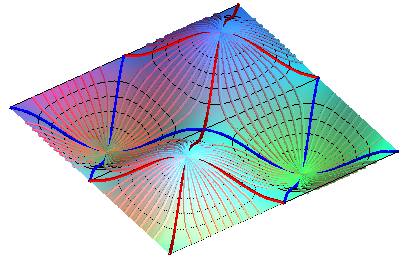
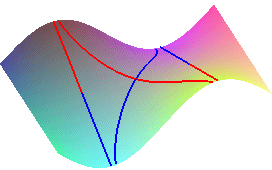
Example: View of the crests (in red) and the thalwegs (in deep blue) of the surface z = y sin x that would stem from this definition, (along with some slope lines, in light blue); note that the crests and thalwegs that lead to the saddle are lines of maximum slope, and do not correspond to the intuitive crests and thalwegs traced on the right!

 

Third definition, by the maximal horizontal curvature, proposed by Gauch in 1993. Given a vertical direction, the crest and thalweg lines are the lines traced on the surface that join the points where the horizontal curvature of the contour line has a maximum. This definition is motivated by the fact that on topographic maps, the contour lines are, in general, curved at the crests and thalwegs, like opposite.

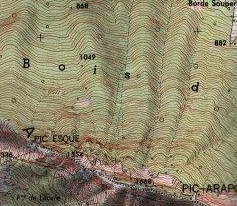The horizontal curvature, the maximum of which has to be determined, is equal to:  (its sign determines the concavity of the point - positive for a convex point, negative for a concave one). Unfortunately, for the surface z = y – x^4 (U-shaped valley), this definition gives, in addition to the central line, that intuitively corresponds to the geographic thalweg, two parallel lines (that are not slope lines), which would yield 3 thalwegs for one valley! Even worse, for the surface z = y – sqrt(1-x^2), the contour lines of which are arcs of circles, every point is an extremum of curvature, and therefore the thalwegs would cover the whole valley!

z = y - x^4: (Fake) thalwegs in deep blue, contour lines in black, slope lines in light blue, normal thalweg in bold black.

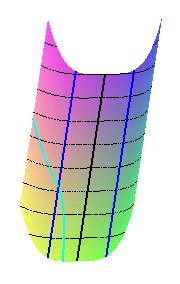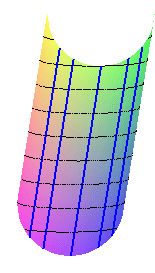z = y - sqrt(1-x^2): with the 3rd definition, all the points of the valley are thalweg points!

Fourth definition (proposed by Boussinesq in 1872 - see below, used in part in the mathematical dictionary of F. Le Lionnais)

The crest and thalweg lines are the slope lines for which the neighbor lines get closer when we travel along them in the direction of the slope (thalweg), or move away (crests).
Indefensible definition since every slope line of a non planar surface would be a crest or a thalweg !

Fifth definition (proposed by Rothe in 1915).
The crest and thalweg lines are the singular slope lines, in the sense that they correspond to the singular solutions of the differential equation of the horizontal projections of the slope lines.
 

Using the Monge notations, the differential equation of the slope lines of the surface z = f(x,y) being qdx - pdy = 0, the crest and thalweg lines are composed of the set of points where u is equal to zero or undefined, where u is defined by u(qdx - pdy) = dF. For example for the surface z = y sin x , qdx - pdy= sinx dx - y cos x dy and d F = d (exp(x²) cos²x)= -2 exp(y²)cosx (qdx - pdy). The singular solutions are given by u = 0, i.e. cos x = 0 i.e. x = pi/2 + kpi. This definition has the defect of not being a geometric definition and not necessarily yields slope lines starting from a saddle...

Sixth definition:
The thalweg and crest lines are the slope lines that also are curvature lines of the surface (lines tangent to a principal direction, where the curvature is extreme).
It can be proved that these lines correspond to the slope lines the horizontal projection of which is linear, and were already obtained through definition #2.

All in all, there only is a consensus about the linearity of the projections of the slope lines!

Examples:
- the crest and thalweg lines of a surface of revolution with vertical axis are the meridians (if we use the definition in a large sense; in the strict sense, there aren't any)
- the crest and thalweg lines of a cone with vertical direction are the generatrices that intersect perpendicularly the contour lines (for a cone , this corresponds to the extrema of f).
 
 

Note of Mr J. Boussinesq presented in 1872 at the Académie des Sciences. In a Note dated June 3, 1872 (Comptes rendus, t. LXXIV, P. 1458), Y. C. Jordan tried to give a geometric definition of the crests and the thalwegs, lines that everyone recognizes on the surface of the ground and could trace with little error, but for which we encounter difficulties in determining the precise nature. Mr Jordan thinks: 1° that these lines cannot be distinguished, in their trajectory, from the other lines of maximal slope; 2° that their only peculiar nature lies in their starting point, as the names of crest and thalweg must only be used for the four lines with maximal slope that come off a saddle, two of them (the crests) going up from this point, whereas the other two (the thalwegs) go downwards. Allow me to observe that these two propositions appear to me, for the second one too restrictive, and for the first one in disagreement with the notion of crest and thalweg such as they are, in a more or less clear way, in all minds. Thalwegs and crests can indeed be distinguished among the other lines of maximal slope, because any inhabitant of the mountains can trace easily, with the utmost precision, the thalweg of their valley or the crest that separates the slope they live on and the neighbor slope, with no need to go to the origin, oftentimes very far and almost inaccessible, of these lines, or to observe the circumstances, with very little importance, of the configuration of the ground at this place. Furthermore, if the existence of these lines depended on the existence of a saddle, then most valleys, that do not have a saddle at their origin, but the higher part of which is a sort of amphiteather that lies on the crest of a mountain, would not have a thalweg, and the various valleys that spread around a summit would not be separated from one another by any crest line; such consequences are obviously inadmissible. To determine the real nature of crests and thalwegs, one should begin by considering these lines in the case where they are the most visible, that is to say when they are materialized by two portions of the ground, protruding or going inwards, with opposite slopes and that intersect forming a dihedral angle different from 180 degrees. We see that a line of maximal slope, extended at the top until a crest changes brutally of direction when it reaches it, and coincides, above, with the crest itself; and also that, extended at the bottom until a thalweg, it has there another angular point, and coincides, below, with the thalweg itself. A crest is therefore like an artery whence spread, from the left to the right and along all its length, downwards, an infinite number of ordinary lines of maximal slope, similar to capillaries studied in anatomy; whereas a thalweg is like a vein that receives from left to right, along all its length, the ordinary lines of maximal slopes. This characteristic is modified, but remains highly recognizable, when, in order to obtain a continuous surface, the angular portions of the ground are replaced by smoother parts that diverge a very little from it; then, the lines of maximal slope have, in the loci where they get closer to the crests or the thalwegs, a small arc with a high curvature instead of an angular point, and afterwards they tend to coincide with these lines, from which their distance becomes absolutely imperceptible; at this time, their physical reunion at the crest or the thalweg is completely done, even though, on a geometric or abstract point of view, they continue asymptotically to go up alongside the crest or go down alongside the thalweg, until the topmost end of the first, or the bottommost end of the second, and this also holds, up to the fact that the direction of the lines of maximal slopes vary more gradually from a point to the other, when the surface of the ground has only small curvatures, while assuming nonetheless, as it happens almost everywhere because of the action of water, the shape of juxtaposed creases. In any case, the ground is divided into stretched strips, or mountain sides which are all the geometric loci of a series of adjacent lines of maximal slope on all their length, and that, cutting them transversally, spread from the upper edge, called crest line, to arrive at the lower edge, called thalweg line. To sum up, a crest line is a line whence spread, along all its length, lines of maximal slope that were initially at zero, or imperceptible, distance and that move expand away at noticeable distances; a thalweg is a line on which, at all the points on its length, are reunited, strictly speaking, at least asymptotically, lines of maximal slope that were initially at noticeable distances; such is the characteristic that distinguishes these remarkable lines from the ordinary lines of maximal slope which are, on the contrary, adjacent to their neighbors along all their length.

 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2018