next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

3D BASIN


 


 
 

Projection on a plane containing Oz: 2D basin

Projection on xOy: rose

 
Homemade name.

 
Cartesian parametrization: n > 0.
Cylindrical equation: .

The basin is the image of the cylindrical sine wave: by the map ; geometrically, it is therefore the central projection with respect to O of this wave on the paraboloid of revolution: .

The projections on the planes containing Oz are the 2D basins and the projections on the plane xOy are the roses.
 
 
Animations showing how the 3D basin is the central projection on a paraboloid of a cylindrical sine wave as well as the orthogonal projection of a rose.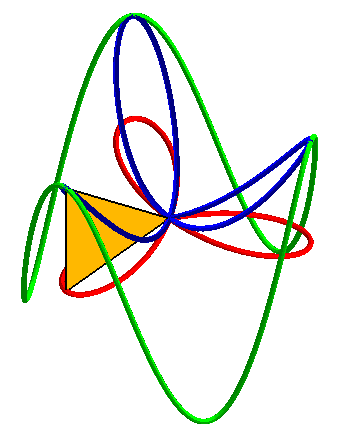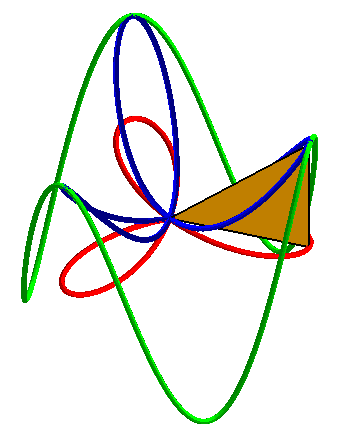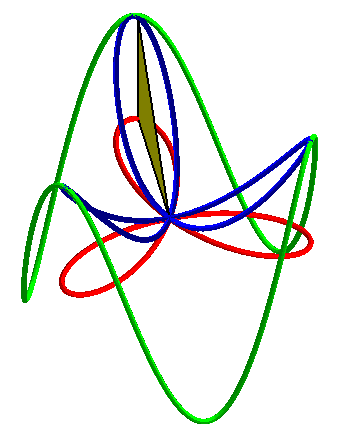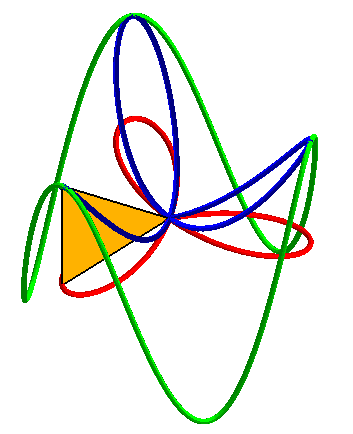
n = 3
n = 2
n = 5/2

 
Remark: for n =1, the basin , traced in the plane bx = az, is none other than an ellipse.

 
In the same way, any curve with polar coordinates can be "lifted on a paraboloid" as .

Here is, for example, a "lift" of a conchoid of a rose.

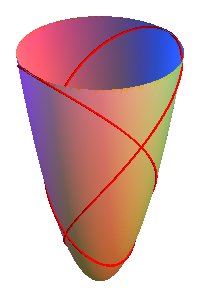Compare to the clelias and the conical roses.
 
next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

© Robert FERRÉOL 2018