Équation intrinsèque :
Paramétrisation :
Prenant
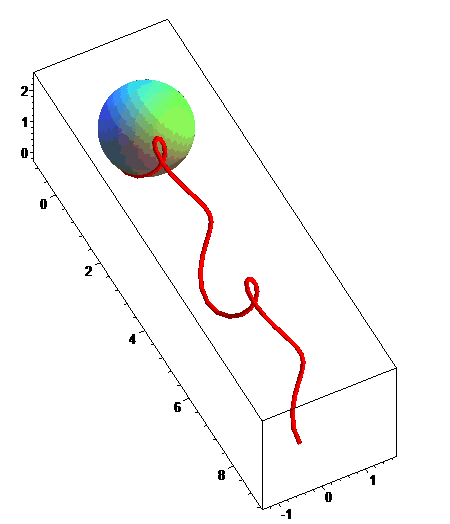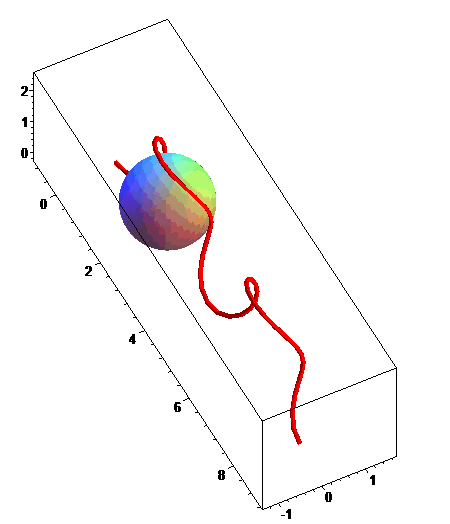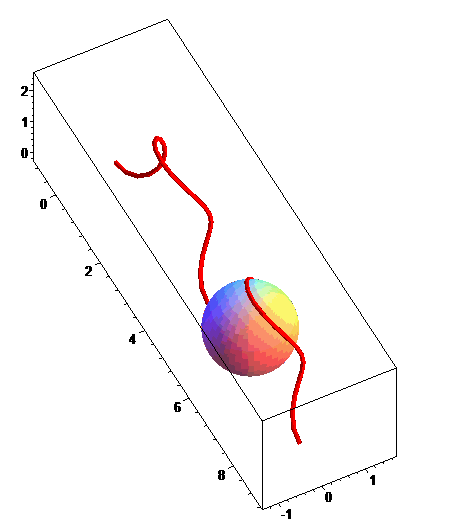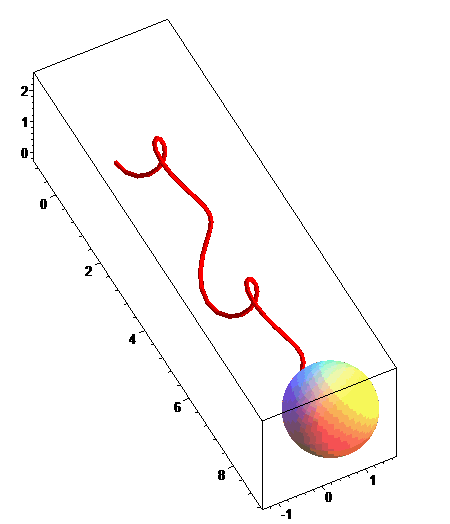
Ci-contre, le cas g(t) = t (l'extrémité
de suivant
donc une courbe de Viviani) avec animation de la sphère
osculatrice.
Avec ,
on obtient :
,
avec
(formules
de Serret).
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
COURBE À COURBURE, ou TORSION CONSTANTE
Skew
circle, schiefer Kreis
1) Courbe à courbure constante (non nulle)
:
| Courbe étudiée par Monge
en 1771, puis par Cesaro en 1896 [geometria intrinseca, p.144].
Autres noms : cercle gauche (nom donné par Cesaro), courbe de Monge. Voir dans la biblio : [Loria 3d] p. 99 , [Brocard Lemoyne t1] p. 356 [teixeira t2] p 441. |
| Voir les notations.
Équation intrinsèque : Paramétrisation : Prenant Ci-contre, le cas g(t) = t (l'extrémité
de Avec |
 |
Une condition nécessaire et suffisante, dans le cas non plan (torsion non nulle) pour qu'une courbe soit à courbure constante est que le rayon de courbure soit égal au rayon de la sphère osculatrice, ou que la sphère osculatrice soit centrée au centre de courbure (voir les notations). Le lieu des centres de courbure est aussi à courbure constante, et le lieu des centres de courbure de cette deuxième courbe est la première courbe.
2) Courbe à torsion constante (non nulle)
:
| Courbe étudiée par Koenigs
en 1887, Cosserat en 1895 (c.r.
acad sciences t. 120), et Gambier
en 1919.
Voir dans la biblio : [Loria 3d] p. 105 , [Brocard Lemoyne t1] p. 427, [Teixeira t2 ] p 445 ; voir aussi l'énoncé de centrale 2 88. |
| Équation intrinsèque : Paramétrisation 1 : prenant Paramétrisation 2 : Prenant 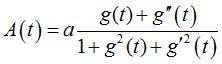 (Formules de Teixeira).
(Formules de Teixeira).
Dans ce cas, le rayon de courbure vaut : |
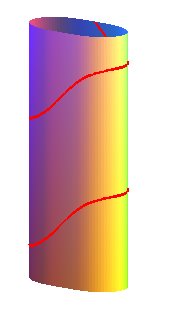
| Le cas g(t) = t dans la paramétrisation
1 donne la courbe : |
 |
| Le cas g(t) = cte dans les formules de
Teixeira donne l'hélice circulaire, et le cas |
 |
L'hélice circulaire (y compris le cercle), est la seule courbe à courbure et torsion constantes.
Les courbes à courbure constante, et celles à torsion constante sont des cas particuliers de courbes de Bertrand (dont la torsion est en relation affine avec la courbure).
Voir aussi les cercles
géodésiques.
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2019