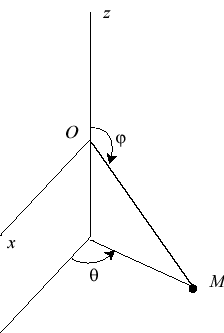
Équation différentielle du mouvement (issue de la relation fondamentale de la dynamique) : . Traduction en coordonnées sphériques  :  où q = longitude, j = colatitude et . Intégrales premières : . Équation différentielle sphérique de la courbe :  (avec ), soit, en posant 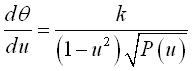 :  où , conduisant à une intégrale elliptique ;  remarquer la minime différence avec la chaînette sphérique, pour laquelle .

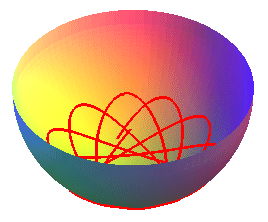
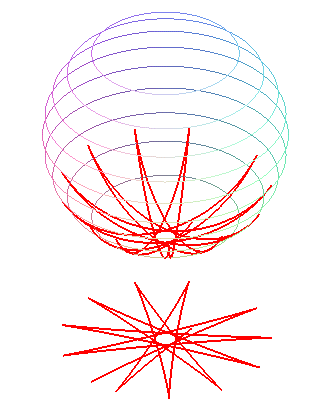
La courbe du pendule sphérique est la courbe décrite par l'extrémité d'un pendule pesant simple attaché à un point fixe, habilité à se mouvoir en 3 dimensions, et placé dans un champ de pesanteur uniforme (ici, ).

Cette courbe est tracée sur une sphère, et n'est autre qu'une ligne d'écoulement de cette sphère : on la réalise donc aussi physiquement en faisant rouler une bille à l'intérieur d'une sphère.

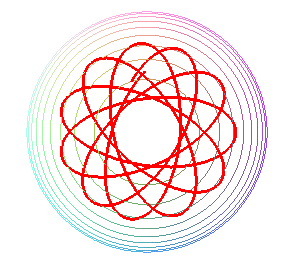
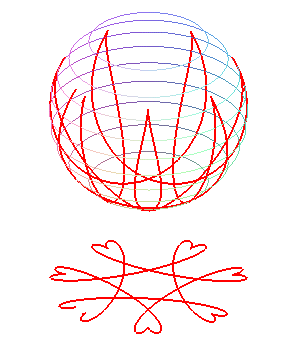
Comme pour les chaînettes sphériques, on  obtient des courbes formées d'une suite d'ondulations joignant alternativement deux parallèles (obtenus pour les valeurs où le polynôme P
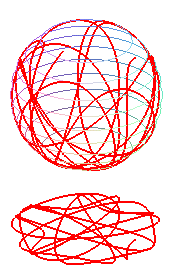
ci-dessus s'annule), et transformées les unes des autres par rotation autour de Oz. La courbe est soit fermée, soit dense dans la zone comprise entre les deux parallèles.

Ces motards acrobates vus au cirque de Shanghai décrivent de telles courbes.
 

On peut généraliser ces courbes en introduisant une force de Coriolis, ce qui donne comme équation différentielle du mouvement : .

Lorsque le pendule est lâché sans vitesse initiale, on obtient alors une courbe du pendule de Foucault, qui, pour de petites oscillations, est approchée par une hypocycloïde.
Sans force de Coriolis, cette courbe se réduirait à un arc de cercle.
 
 

Lorsque le vecteur W n'est pas vertical, la courbe n'est plus à symétrie de rotation autour de Oz.

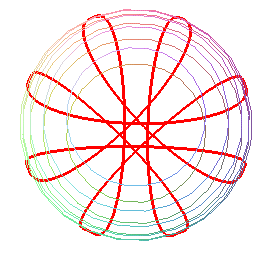
Voici une vue de la courbe décrite par un pendule en rotation forcée uniforme autour de Oz.

Voir les festons de toupie, qui constituent une autre généralisation des courbes du pendule sphérique.
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2004