Cartesian parametrization: . Cartesian equation:  (proving that the contour lines are ellipses), i.e. . Quartic surface. Volume of the milk carton: . Area of the milk carton when k = 1/2: » 7,29a2. The striction line is obtained for , hence the parametrization : .

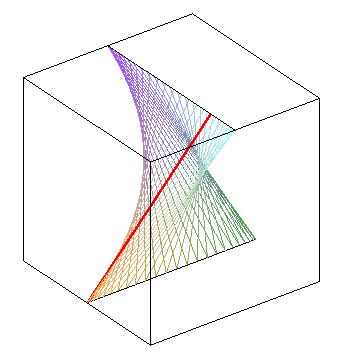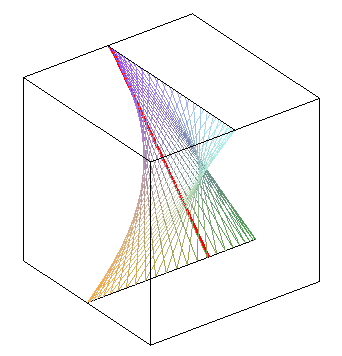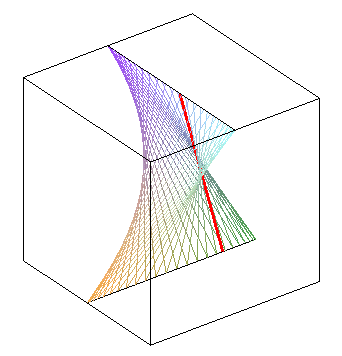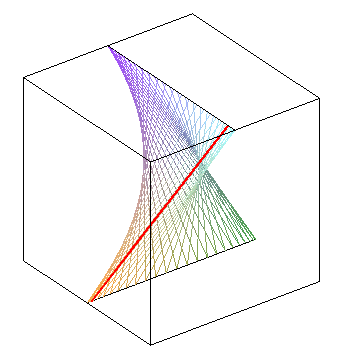
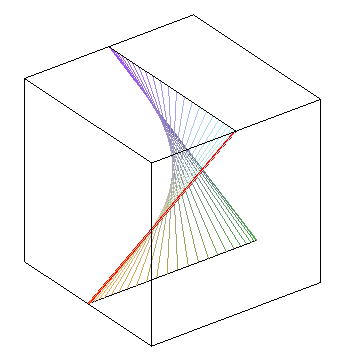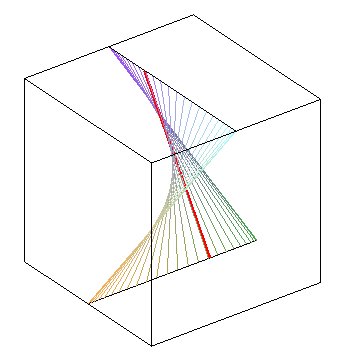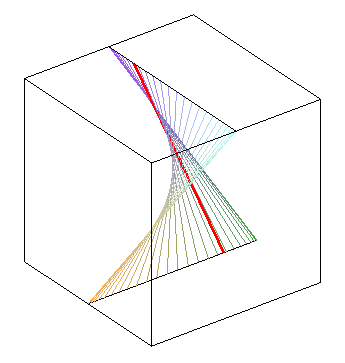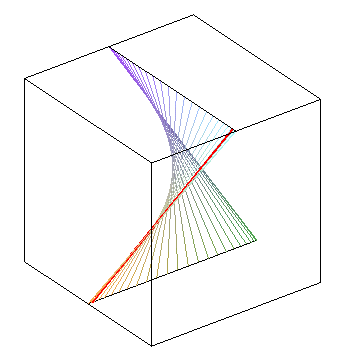
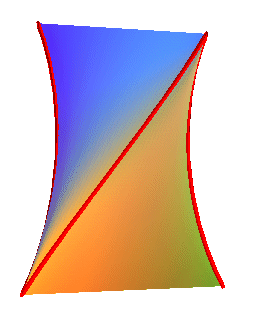Mik carton with his striction line [Aubert Papelier, T 3, p. 132].

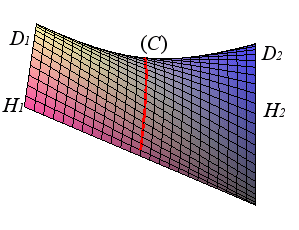
Here, (D₁) is , (D₂) is and the radius of (C) is ka.

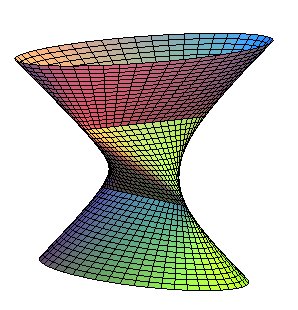
Here is the (more) complete surface:

The lengths of the two double segment lines carried by (D₁) and (D₂) are equal to 4ka.

The milk carton is also the ruled surface generated by the lines (M1M2),  and  with two orthogonal sinusoidal motions in quadrature; the part shaped like a milk carton is the reunion of the segment lines [M1M2]. The length of the segment line [M1M2] then remains constant equal to ; the milk carton can therefore also be defined as the ruled surface generated by a line two fixed points of which slide on two fixed orthogonal non-intersecting lines. All the points on the line describe ellipses (which constitutes a generalization of the Proclus ellipsograph).

The projection of the segment line [M1M2] on xOy also maintains a constant length: the view from above of a milk carton is therefore a full astroid.

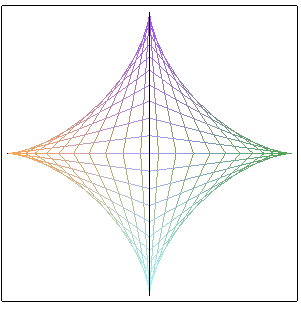We also get a generalization of the milk carton by considering the conoidal surface generated by the lines (M₁M₂), ,  having two orthogonal sinusoidal motions with any phase difference ( for the milk carton).
 

phase difference equal to	zero phase difference: we get a hyperbolic paraboloid	phase opposition: another hyperbolic paraboloid

 

Be careful, a milk carton like the one opposite made of paper is a developable surface, made from a tetrahedron template by bending the edges...

Compare to the conocuneus, as well as the Cayley cubic surface.
 

next surface

previous surface

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL, Alain ESCULIER 2022