ELLIPTICAL CONE

| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
ELLIPTICAL CONE

| Other name: degree-two cone (implying: non-decomposed). |
| Reduced equation: Sections by the plane z = k are ellipses with half-axes ak/h and bk/h. Developable ruled quadric. Cartesian parametrization: Parametrization for which the coordinate lines are the curvature lines (case Half major angle at the vertex: Half minor angle at the vertex: Volume of the solid between the planes z=0 and
z=h
: |
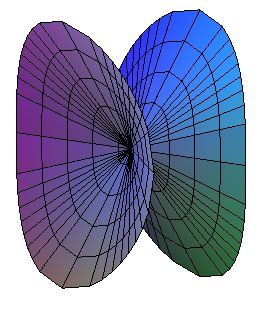 |
An elliptical cone is a cone a directrix of which is an ellipse; it is defined up to isometry by its two angles at the vertex.
Characterization: cone of degree two not decomposed into
two planes.
| Contrary to appearances, every elliptical cone contains
circles.
If we turn the plane z = h by an angle Thus, the elliptical cone is also an oblique circular cone. |
 |
See the level and slope lines of the cone here.
See also focal
circular cubic.
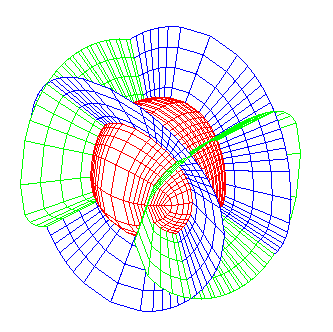
Triple
orthogonal system two families of which are composed of elliptic cones
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2020