Henneberg's surface

HENNEBERG'S SURFACE

Surface studied by Henneberg in 1875, but one will find out on this page that Catalan already knew this surface in 1858, which he presents as the first known minimal surface that is algebraic.
Lebrecht Henneberg (1850 - 1923): German mathematician.

Cartesian parametrization: .
Algebraic minimal surface.

Henneberg's surface is the minimal surface obtained by taking (and then ) in the Weierstrass parametrization of a minimal surface: .

It constitutes a model of the projective plane; it is therefore a one-sided surface, and we can trace a Möbius strip on it as one can see opposite.

The coordinate line obtained for v = 0 is a semicubical parabola, with equation ; it is a geodesic of the surface which makes Henneberg's surface a Björling surface associated to a semicubical parabola.
Since the surface is invariant by a rotoreflection with axis Oz, angle and plane xOy, there is a second semicubical parabola, as one can see opposite.

The surfaces "associated" to Henneberg's surface, obtained by taking are parametrized by:

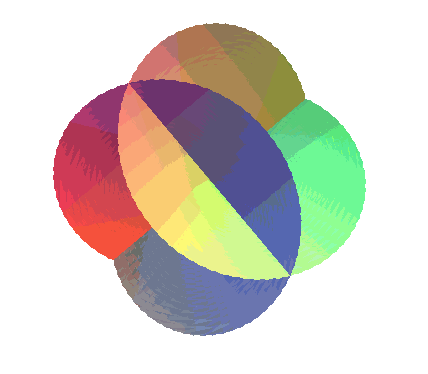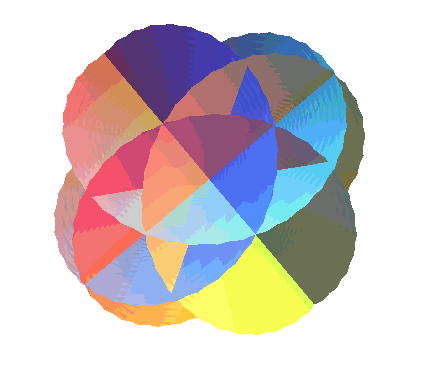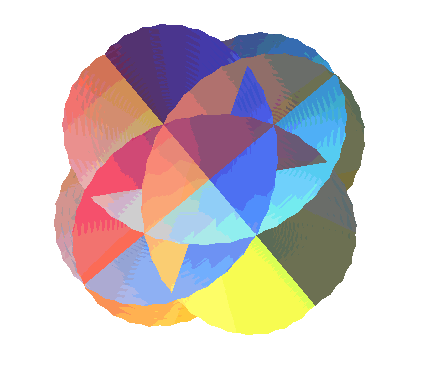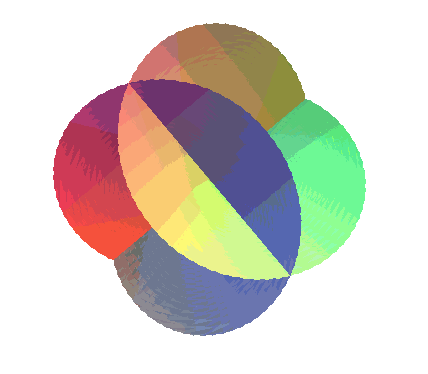Engraving of Henneberg's surface, by Patrice Jeener, with his kind authorization.

next surface previous surface 2D curves 3DÂ curves surfaces fractals polyhedra

It constitutes a model of the projective plane; it is therefore a one-sided surface, and we can trace a Möbius strip on it as one can see opposite.
The coordinate line obtained for v = 0 is a semicubical parabola, with equation ; it is a geodesic of the surface which makes Henneberg's surface a Björling surface associated to a semicubical parabola. Since the surface is invariant by a rotoreflection with axis Oz, angle and plane xOy, there is a second semicubical parabola, as one can see opposite.
The surfaces "associated" to Henneberg's surface, obtained by taking are parametrized by: